题目内容
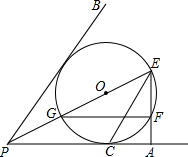 (2012•湖北模拟)如图,点O在∠APB的平分线上,⊙O与PA边相切于点C,
(2012•湖北模拟)如图,点O在∠APB的平分线上,⊙O与PA边相切于点C,(1)求证:PB是⊙O的切线;
(2)PO的延长线交⊙O于E,EA⊥PA于A.设PE交⊙O于另一点G,AE交⊙O于点F,连接FG,若⊙O的半径是3,
| AC |
| AE |
| 1 |
| 2 |
①求弦CE的长;②求
| FG |
| PA |
分析:(1)连接OC,过点O作OD⊥PB于点D,根据切线的定义可得OC⊥PA,根据角平分线上的点到角的两边的距离相等可得OC=OD,再根据切线的定义判定即可;
(2)①连接CG,根据垂直的定义可得∠AEC+∠ECA=90°,再根据切线的定义可得OC⊥PA,然后求出∠OCE+∠EAC=90°,然后求出∠OCE=∠CEA,再根据等边对等角可得∠OCE=∠OEC,从而得到∠AEC=∠CEG,再根据直径所对的圆周角是直角求出∠ECG=90°,然后利用∠AEC和∠CEG的正切值相等列式求解即可得到
=
,然后设CG=x,表示出CE=2x,在Rt△CEG中,利用勾股定理列式计算即可求出x,然后求出CE即可;
②根据同角的余角相等求出∠PCG=∠CEG,然后求出△PCG和△PEC相似,再根据相似三角形对应边成比例求出
=
=
,然后设PG=m,表示出PC=2m,在Rt△POC中,利用勾股定理列式求出m的值,再求出△EGF和△EPA相似,利用相似三角形对应边成比例列式计算即可得解.
(2)①连接CG,根据垂直的定义可得∠AEC+∠ECA=90°,再根据切线的定义可得OC⊥PA,然后求出∠OCE+∠EAC=90°,然后求出∠OCE=∠CEA,再根据等边对等角可得∠OCE=∠OEC,从而得到∠AEC=∠CEG,再根据直径所对的圆周角是直角求出∠ECG=90°,然后利用∠AEC和∠CEG的正切值相等列式求解即可得到
| CG |
| CE |
| 1 |
| 2 |
②根据同角的余角相等求出∠PCG=∠CEG,然后求出△PCG和△PEC相似,再根据相似三角形对应边成比例求出
| PG |
| PC |
| CG |
| CE |
| 1 |
| 2 |
解答: (1)证明:如图,连接OC,过点O作OD⊥PB于点D,
(1)证明:如图,连接OC,过点O作OD⊥PB于点D,
∵PA切⊙O于点C,
∴OC⊥PA,
∵PO平分∠BPA,
∴OC=OD,
∴PB是⊙O的切线;
(2)解:①连接CG,
∵EA⊥PA于A,
∴∠AEC+∠ECA=90°,
∵OC⊥PA,
∴∠OCE+∠EAC=90°,
∴∠OCE=∠CEA,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠AEC=∠CEG,
∵EG为⊙O的直径,
∴∠ECG=90°,
∵tan∠AEC=
=
,
∴tan∠CEG=
=
,
设CG=x,则CE=2x,
∵⊙O的半径为3,
∴直径EG=6 ,
,
∴x2+(2x)2=62,
解之得,x1=
,x2=-
(不合题意,舍去),
∴x=
,CE=2x=
;
②∵OC⊥PA,
∴∠OCG+∠PCG=90°,
∵OC=OE,
∴∠OCG=∠OGC=∠ECG=90°,
∴∠OGC+CEG=90°,
∴∠PCG=∠CEG,
∵∠EPC=∠CPG,
∴△PCG∽△PEC,
∴
=
=
,
设PG=m,则PC=2m,在Rt△POC中,OG=OC=3,
根据勾股定理,PC2+OC2=PO2,
即(2m)2+32=(m+3)2,
解得m1=2,m2=0(舍去),
∵∠GFE=∠PAE=90°,
∴GF∥PA,
∴△EGF∽△EPA,
∴
=
=
=
.
 (1)证明:如图,连接OC,过点O作OD⊥PB于点D,
(1)证明:如图,连接OC,过点O作OD⊥PB于点D,∵PA切⊙O于点C,
∴OC⊥PA,
∵PO平分∠BPA,
∴OC=OD,
∴PB是⊙O的切线;
(2)解:①连接CG,
∵EA⊥PA于A,
∴∠AEC+∠ECA=90°,
∵OC⊥PA,
∴∠OCE+∠EAC=90°,
∴∠OCE=∠CEA,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠AEC=∠CEG,
∵EG为⊙O的直径,
∴∠ECG=90°,
∵tan∠AEC=
| AC |
| AE |
| 1 |
| 2 |
∴tan∠CEG=
| CG |
| CE |
| 1 |
| 2 |
设CG=x,则CE=2x,
∵⊙O的半径为3,
∴直径EG=6
 ,
,∴x2+(2x)2=62,
解之得,x1=
6
| ||
| 5 |
6
| ||
| 5 |
∴x=
6
| ||
| 5 |
12
| ||
| 5 |
②∵OC⊥PA,
∴∠OCG+∠PCG=90°,
∵OC=OE,
∴∠OCG=∠OGC=∠ECG=90°,
∴∠OGC+CEG=90°,
∴∠PCG=∠CEG,
∵∠EPC=∠CPG,
∴△PCG∽△PEC,
∴
| PG |
| PC |
| CG |
| CE |
| 1 |
| 2 |
设PG=m,则PC=2m,在Rt△POC中,OG=OC=3,
根据勾股定理,PC2+OC2=PO2,
即(2m)2+32=(m+3)2,
解得m1=2,m2=0(舍去),
∵∠GFE=∠PAE=90°,
∴GF∥PA,
∴△EGF∽△EPA,
∴
| FG |
| PA |
| EG |
| EP |
| 6 |
| 6+2 |
| 3 |
| 4 |
点评:本题考查了圆的综合题型,主要利用了圆的切线的定义与判定,角平分线上的点到角的两边的距离相等的性质,直径所对的圆周角是直角,相似三角形的判定与性质,勾股定理的应用,综合题,但难度不大,仔细分析便不难求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•湖北模拟)如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°.翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点F、E,若AD=2,BC=8,
(2012•湖北模拟)如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°.翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点F、E,若AD=2,BC=8, (2012•湖北模拟)如图,一次函数y=mx+5的图象与反比例函数
(2012•湖北模拟)如图,一次函数y=mx+5的图象与反比例函数