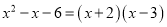题目内容
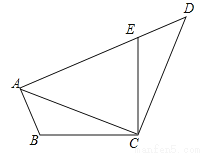
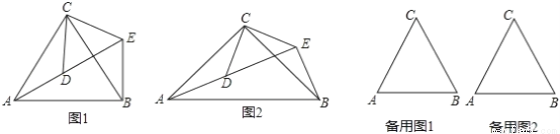
如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.
【答案】(1)证明见解析;(2)112.5°.
【解析】试题分析:  根据同角的余角相等可得到
根据同角的余角相等可得到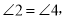 结合条件
结合条件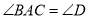 ,再加上
,再加上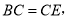 可证得结论;
可证得结论;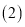 根据
根据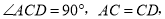 得到
得到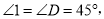 根据等腰三角形的性质得到
根据等腰三角形的性质得到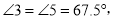 由平角的定义得到
由平角的定义得到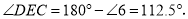
试题解析:  证明:
证明:
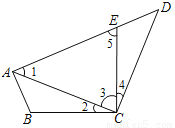
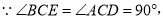
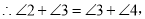
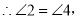
在△ABC和△DEC中,  ,
,
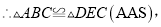
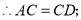
(2)∵∠ACD=90°,AC=CD,
∴∠1=∠D=45°,
∵AE=AC,
∴∠3=∠5=67.5°,
∴∠DEC=180°-∠5=112.5°.
【题型】解答题
【结束】
21
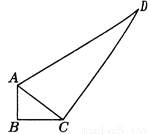
一个零件的形状如图所示,工人师傅按规定做得∠B=90°,
AB=3,BC=4,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


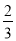 ,该老板到底给顾客优惠了吗?说出你的理由.
,该老板到底给顾客优惠了吗?说出你的理由.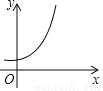 B.
B. 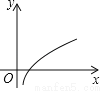 C.
C. 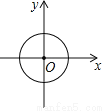 D.
D. 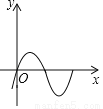
 ,
, ,
,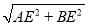 =17;
=17;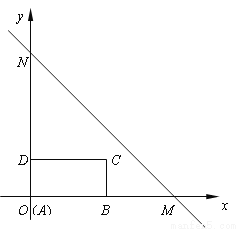
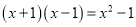 B.
B. 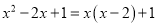
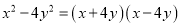 D.
D.