题目内容
已知△ABC的一边AC为关于x的一元二次方程x2+mx+5=0的两个正整数根之一，且另两边长为BC=3，AB=5，求cosA．
∵AC为x2+mx+5=0的两个正整数根之一，则两根的积是5，
∴AC≤5，
∵BC=3，AB=5，
∴5-3＜AC＜5+3，即2＜AC＜8，
∴2＜AC≤5，
∴AC=3或4或5．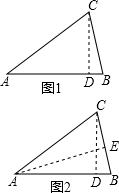
作CD⊥AB于点D，如图1，
AC=3时，AC=BC，
∴AD=
AB=
×5=
，cosA=
=
=
；
当AC=4时，△ABC是直角三角形，∠C=90°，则cosA=
=
；
当AC=5时，作CD⊥AB于点D，作AE⊥BC于点E，如图2．
则CE=
BC=
，
在直角△ACE中，AE=
=
，
∵2SABC=AE•BC=AB•CD，
∴CD=
=
=
，
∴AD=
=
，
∴cosA=
=
=
．
∴AC≤5，
∵BC=3，AB=5，
∴5-3＜AC＜5+3，即2＜AC＜8，
∴2＜AC≤5，
∴AC=3或4或5．
作CD⊥AB于点D，如图1，
AC=3时，AC=BC，
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| AD |
| AC |
| ||
| 3 |
| 5 |
| 6 |
当AC=4时，△ABC是直角三角形，∠C=90°，则cosA=
| AC |
| AB |
| 4 |
| 5 |
当AC=5时，作CD⊥AB于点D，作AE⊥BC于点E，如图2．
则CE=
| 1 |
| 2 |
| 3 |
| 2 |
在直角△ACE中，AE=
| AC2-CE2 |
| ||
| 2 |
∵2SABC=AE•BC=AB•CD，
∴CD=
| AE•BC |
| AB |
3×
| ||||
| 5 |
3
| ||
| 10 |
∴AD=
| AC2-CD2 |
| ||
| 10 |
∴cosA=
| AC |
| AB |
| ||||
| 5 |
| ||
| 50 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
