题目内容
k取何值时,直线y=3x+k+2与直线y=-x+2k的交点在第二象限.分析:首先求出方程组
的解,然后根据第二象限内点的坐标特征,列出关于k的不等式组,从而得出k的取值范围.
|
解答:解:解方程组
,
得
,
∵交点在第二象限,
∴
,
解得:-
<k<2.
故k的取值范围是:-
<k<2.
|
得
|
∵交点在第二象限,
∴
|
解得:-
| 2 |
| 7 |
故k的取值范围是:-
| 2 |
| 7 |
点评:本题主要考查了一次函数与方程组的关系及第二象限内点的坐标特征,难度适中,关键掌握两个一次函数图象的交点坐标就是对应的二元一次方程组的解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
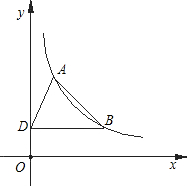 点B作y轴的垂线,垂足为D,连接AD.
点B作y轴的垂线,垂足为D,连接AD. 果存在,求出t的值;如果不存在,请说明理由.
果存在,求出t的值;如果不存在,请说明理由. 如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线l过点A(-1,0),与y轴交于B(m,0),
如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线l过点A(-1,0),与y轴交于B(m,0),