题目内容
10．抛物线y=x2-2x-8与x轴的交点坐标是（4，0）（-2，0）．分析 要求抛物线与x轴的交点，即令y=0，解方程即可．
解答 解：令y=0，则x2-2x-8=0．
（x-4）（x+2）=0
解得x=4或x=-2．
则抛物线y=x2-2x-8与x轴的交点坐标是（4，0），（-2，0）．
故答案为：（4，0），（-2，0）．
点评 本题考查了抛物线与x轴的交点．关键是掌握求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标，令y=0，即ax2+bx+c=0，解关于x的一元二次方程即可求得交点横坐标．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
20．一小商店一周的盈亏情况如表（亏为负），单位：元
（1）计算出小商店一周的盈亏情况；
（2）指出盈利最多一天的盈利额．
| 星期 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| 盈亏情况 | 128.3 | -25.6 | -15 | 27 | -7 | 36.5 | 98 |
（2）指出盈利最多一天的盈利额．
18．如图是2015年12月月历．
（1）如图，用一正方形框在表中任意框住4个数，记左上角的一个数为x，则另三个数用含x的式子表示出来，从小到大依次是x+1，x+7，x+8．
（2）在表中框住四个数之和最小记为a1，和最大记为a2，则a1+a2=128．
（3）当（1）中被框住的4个数之和等于76时，x的值为多少？
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
（2）在表中框住四个数之和最小记为a1，和最大记为a2，则a1+a2=128．
（3）当（1）中被框住的4个数之和等于76时，x的值为多少？
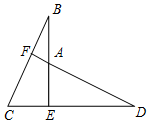已知：BE⊥CD，BE=DE，BC=DA，求证：AE=CE．
如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，