Question

11．如图，矩形ABCD的对角线AC与BD相交于点O，CE∥BD，DE∥AC，AD=2$\sqrt{3}$，DE=2，则四边形OCED的面积为（　　）

• A． 2$\sqrt{3}$
• B． 4
• C． 4$\sqrt{3}$
• D． 8

Answer 1

分析 连接OE，与DC交于点F，由四边形ABCD为矩形得到对角线互相平分且相等，进而得到OD=OC，再由两组对边分别平行的四边形为平行四边形得到ODEC为平行四边形，根据邻边相等的平行四边形为菱形得到四边形ODEC为菱形，得到对角线互相平分且垂直，求出菱形OCED的面积即可．

解答 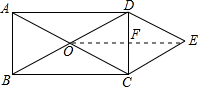解：连接OE，与DC交于点F，
∵四边形ABCD为矩形，
∴OA=OC，OB=OD，且AC=BD，即OA=OB=OC=OD，
∵OD∥CE，OC∥DE，
∴四边形ODEC为平行四边形，
∵OD=OC，
∴四边形ODEC为菱形，
∴DF=CF，OF=EF，DC⊥OE，
∵DE∥OA，且DE=OA，
∴四边形ADEO为平行四边形，
∵AD=2$\sqrt{3}$，DE=2，
∴OE=2$\sqrt{3}$，即OF=EF=$\sqrt{3}$，
在Rt△DEF中，根据勾股定理得：DF=$\sqrt{4-3}$=1，即DC=2，
则S_菱形ODEC=$\frac{1}{2}$OE•DC=$\frac{1}{2}$×2$\sqrt{3}$×2=2$\sqrt{3}$．
故选A

点评 此题考查了矩形的性质，菱形的判定与性质，以及勾股定理，熟练掌握矩形的性质是解本题的关键．