题目内容
如图，四边形ABDC中，△EDC是由△ABC绕顶点C旋转40°所得，顶点A恰好转到AB上一点E的位置，则∠1+∠2= 度．
【答案】分析：由旋转的性质可知AC=EC，BC=DC，∠BCD=∠ACE=40°，在△BCD中，由内角和定理求∠1，根据外角定理可求∠1．
解答：解：在△BCD中，∠BCD=∠ACE=40°，BC=CD，
∴△BCD为等腰三角形，
∴∠1=
（180°-40°）=70°，
∵∠BEC为△ACE的外角，
∴∠2+∠DEC=∠ACE+∠A，而∠DEC与∠A为对应角，
∴∠2=∠ACE=40°，
∴∠1+∠2=70°+40°=110°．
故答案为：110°．
点评：本题考查了旋转的性质的运用．旋转前后对应边相等，对应点与旋转中心的连线相等，且夹角为旋转角．
解答：解：在△BCD中，∠BCD=∠ACE=40°，BC=CD，
∴△BCD为等腰三角形，
∴∠1=
（180°-40°）=70°，∵∠BEC为△ACE的外角，
∴∠2+∠DEC=∠ACE+∠A，而∠DEC与∠A为对应角，
∴∠2=∠ACE=40°，
∴∠1+∠2=70°+40°=110°．
故答案为：110°．
点评：本题考查了旋转的性质的运用．旋转前后对应边相等，对应点与旋转中心的连线相等，且夹角为旋转角．
练习册系列答案
发散思维新课堂系列答案
相关题目
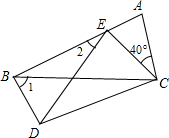如图，四边形ABDC中，△EDC是由△ABC绕顶点C旋转40°所得，顶点A恰好转到AB上一点E的位置，则∠1+∠2=
如图，四边形ABDC、CDFE、EFHG都是正方形．
如图，四边形ABDC内接于⊙O，若∠BOC=120°，则∠A度数为（ ）| A、60° | B、120° | C、80° | D、100° |
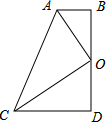如图，四边形ABDC中，∠D=∠ABD=90゜，点D为BD的中点，且OA平分∠BAC．
如图，四边形ABDC中，∠ABD=∠ACD=90゜，BD=CD，求证：AD⊥BC．