题目内容
 如图,四边形ABDC中,∠ABD=∠ACD=90゜,BD=CD,求证:AD⊥BC.
如图,四边形ABDC中,∠ABD=∠ACD=90゜,BD=CD,求证:AD⊥BC.分析:先由条件可以得出根据HL可以△ABD≌△ACD,可以得出AB=AC,∠BAD=∠CAD,就可以得出△ABE≌△ACE就可以得出∠AEB=∠AEC就可以得出结论.
解答:证明:∵∠ABD=∠ACD=90゜,
∴△ABD和△ACD是直角三角形.
在Rt△ABD和Rt△ACD中
,
∴Rt△ABD≌Rt△ACD(HL),
∴AB=AC,∠BAD=∠CAD.
在△ABE和△ACE中
,
∴△BDF≌△CDE (SAS),
∴∠AEB=∠AEC.
∵∠AEB+∠AEC=180°,
∴∠AEB=90°.
∴AD⊥BC.
∴△ABD和△ACD是直角三角形.
在Rt△ABD和Rt△ACD中
|
∴Rt△ABD≌Rt△ACD(HL),
∴AB=AC,∠BAD=∠CAD.

在△ABE和△ACE中
|
∴△BDF≌△CDE (SAS),
∴∠AEB=∠AEC.
∵∠AEB+∠AEC=180°,
∴∠AEB=90°.
∴AD⊥BC.
点评:本题考查了直角三角形的判定及性质的运用,三角形全等的判定及性质的运用,垂直的判定的运用,解答时先证明Rt△ABD≌Rt△ACD是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,四边形ABDC内接于⊙O,若∠BOC=120°,则∠A度数为( )
如图,四边形ABDC内接于⊙O,若∠BOC=120°,则∠A度数为( )| A、60° | B、120° | C、80° | D、100° |
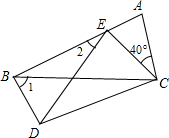 如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2=
如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2= 如图,四边形ABDC、CDFE、EFHG都是正方形.
如图,四边形ABDC、CDFE、EFHG都是正方形.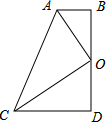 如图,四边形ABDC中,∠D=∠ABD=90゜,点D为BD的中点,且OA平分∠BAC.
如图,四边形ABDC中,∠D=∠ABD=90゜,点D为BD的中点,且OA平分∠BAC.