题目内容
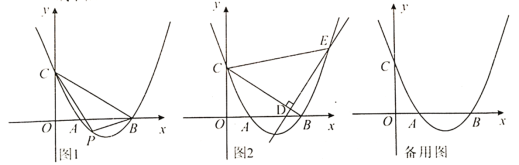
【题目】抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 为线段
为线段![]() 下方抛物线上一动点,连接
下方抛物线上一动点,连接![]() .
.
(1)求抛物线解析式;
(2)在点![]() 移动过程中,
移动过程中,![]() 的面积是否存在最大值?若存在,求出最大面积及点
的面积是否存在最大值?若存在,求出最大面积及点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
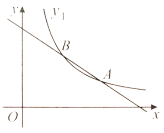
(3)设点![]() 为
为![]() 上不与端点重合的一动点,过点
上不与端点重合的一动点,过点![]() 作线段
作线段![]() 的垂线,交抛物线于点
的垂线,交抛物线于点![]() ,若
,若![]() 与
与![]() 相似,请直接写出点
相似,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ;(3)
;(3)![]() ,
,![]() ,
,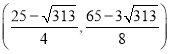
【解析】
(1)由题意设![]() ,结合抛物线
,结合抛物线![]() ,从而可得答案;
,从而可得答案;
(2)过![]() 作
作![]() 轴,交
轴,交![]() 于
于![]() 设点
设点![]() 的坐标为
的坐标为![]() ,表示
,表示![]() 的坐标,求解
的坐标,求解![]() 长度,利用
长度,利用![]() 可得答案;
可得答案;
(3)分情况讨论:当![]() 时,过
时,过![]() 作
作![]() 交
交![]() 于
于![]() ,求解
,求解![]() 的坐标,利用函数的交点求解
的坐标,利用函数的交点求解![]() 的坐标,当过点
的坐标,当过点![]() 作
作![]() ,则有
,则有![]() ,利用二次函数的对称性可得答案,当作
,利用二次函数的对称性可得答案,当作![]() 的垂直平分线,交抛物线于点
的垂直平分线,交抛物线于点![]() ,则有
,则有![]() ,利用函数的交点求得
,利用函数的交点求得![]() 的坐标.
的坐标.
解:(1)![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
![]() 设抛物线的解析式为
设抛物线的解析式为![]()
![]()
![]() ,
,
![]()
![]()
![]() 抛物线解析式为:
抛物线解析式为:![]()
(2)存在,理由如下:过![]() 作
作![]() 轴,交
轴,交![]() 于
于![]()
设点![]() 的坐标为
的坐标为![]() ,
,
![]() 抛物线解析式为:
抛物线解析式为:![]()
![]()
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
设直线![]() 的解析式为:
的解析式为:![]()
![]()
解得: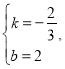
![]() 直线
直线![]() 的解析式为
的解析式为![]()
故点![]() 的坐标为
的坐标为![]()
![]()
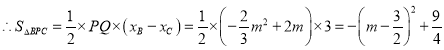
故当![]() 时,
时,![]() 有最大值为
有最大值为![]()
此时点![]() 的坐标为
的坐标为![]()

(3)点![]() 的坐标为
的坐标为![]() ;
;![]() ;
;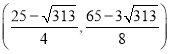 ;
;
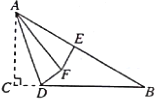
理由如下:如图4,![]() ,可得
,可得![]() ;
;
同上可知线段![]() 的解析式为
的解析式为![]() ,
,
过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
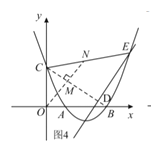
![]() 直线
直线![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
联立方程组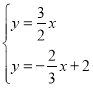 ,
,
解得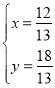
解得点![]() 的坐标为
的坐标为![]() ,
,
故点![]() 关于
关于![]() 的对称点
的对称点![]() 的坐标为
的坐标为![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
设直线![]() 的解析式为:
的解析式为:![]() ,
,
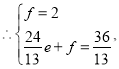
解得:
![]() 直线
直线![]() 的解析式为
的解析式为![]()
将![]() 与
与![]() 联立方程可得:
联立方程可得:
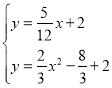 ,解得
,解得 (舍),
(舍),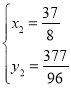 ,
,
故点![]() 的坐标为
的坐标为![]() ;
;
如图5,过点![]() 作
作![]() ,
,
![]()
![]()
![]()
![]() ,
,
此时点![]() 关于抛物线
关于抛物线![]() 的对称轴
的对称轴![]() 对称,
对称,
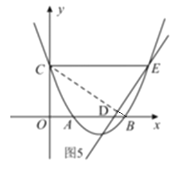
![]() 点
点![]() 的坐标为
的坐标为![]() ,故此时点
,故此时点![]() 的坐标为
的坐标为![]()
如图6,作![]() 的垂直平分线,交抛物线于点
的垂直平分线,交抛物线于点![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
![]() 中点
中点![]() 的坐标为
的坐标为![]() ,
,
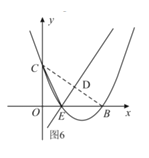
![]() 直线
直线![]() ,并经过点
,并经过点![]() ,
,
![]()
设直线![]() 的解析式为:
的解析式为:![]()
![]()
![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 与
与![]()
联立方程组可得
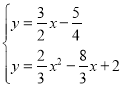 ,
,
解得 ,
,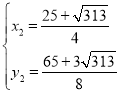 (舍)
(舍)
故点![]() 的坐标为
的坐标为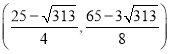
综上可得点![]() 的坐标为:
的坐标为:![]() ;
;![]() ;
;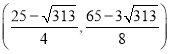

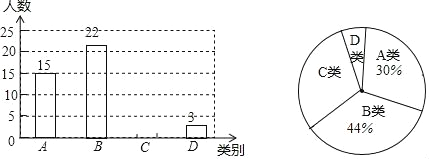
【题目】为了解九年级女生体质健康变化的情况,体育李老师本学期从九年级全体240名女生中随机抽取20名女生进行体质测试,并调取这20名女生上学期的体质测试成绩进行对比,李老师对两次数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a. 两次测试成绩(百分制)的频数分布直方图如下(数据分组:60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
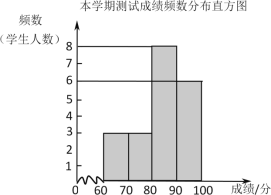
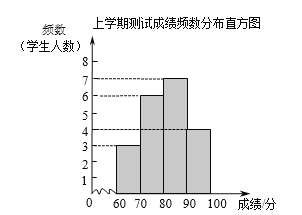
b.成绩在80≤x<90的是:
上学期:80 81 85 85 85 86 88
本学期:80 82 83 86 86 86 88 89
c. 两个学期样本测试成绩的平均数、中位数、众数如下:
学期 | 平均数 | 中位数 | 众数 |
上学期 | 84 | a | 85 |
本学期 | b | c | d |
根据以上信息,回答下列问题:
(1)表中a的值是 ;
(2)下列关于本学期样本测试成绩的结论:①c=86;②d=86;③成绩的极差可能为41;④b有可能等于80.其中所有正确结论的序号是 ;
(3)从两个不同角度分析这20名女生从上学期到本学期体质健康变化情况.