Question

【题目】如图，一次函数的图象与x轴、y轴分别交于A、B，以线段AB为直角边在第一象限内作Rt△ABC，且使∠ABC=30°。

（1）求AC的长度；

（2）如果在第二象限内有一点，试求四边形AOPB的面积S与m之间的函数关系式，并求当△APB与△ABC面积相等时m的值。

（3）是否存在使△QAB是等腰三角形并且在坐标轴上的点Q？若存在，请写出点Q所有可能的坐标；若不存在，请说明理由。

Answer 1

【答案】（1）AC=；（2）m＝；（3）（0，2），（0，＋2），（1，0）（3，0），（0，），（0，）

【解析】

（1）先求出A、B两点的坐标，再由一个角等于30°，即可求出AC的长；

（2）过P作PD⊥x轴，垂足为D，先求出梯形ODPB的面积和△AOB的面积之和，再减去△APD的面积，即是△APB的面积；根据△APB与△ABC面积相等，求得m的值；

（3）假设存在点Q，使△QAB是等腰三角形，分情况求出Q点的坐标即可．

（1）∵一次函数的解析式为函数图象与x轴、y轴分别交于点A、B，

∴A（1，0），B（0，），

∴AB＝2，

设AC＝x，则BC＝2x，由勾股定理得，4x2x2＝4，

解得x＝

则AC=；

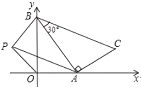
（2）过P作PD⊥x轴，垂足为D，

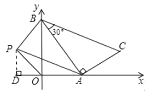
S△APB＝S梯形ODPB＋S△AOBS△APD＝

=，

∵S△ABC=

∴=

解得m＝；

（3）∵AB＝=2，

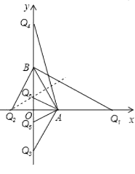
∴如图：当AQ＝AB时，点Q1（3，0），Q2（1，0），Q3（0，）；

当AB＝BQ时，点Q4（0，＋2），Q5（0，2），Q2（1，0）；

当AQ＝BQ时，点Q6（0，），Q2（1，0），

综上可得：（0，2），（0，＋2），（1，0）（3，0），（0，），（0，）