题目内容
计算:
(1)8a+7b-12a-5b
(2)(5mn-2m+3n)+(-7m-7mn)
(3)3(x2y-4xy2)-5(x2y-
xy2)
(4)5a2b-[2ab2-3(ab2-a2b)].
(1)8a+7b-12a-5b
(2)(5mn-2m+3n)+(-7m-7mn)
(3)3(x2y-4xy2)-5(x2y-
| 1 |
| 5 |
(4)5a2b-[2ab2-3(ab2-a2b)].
考点:整式的加减
专题:
分析:(1)直接合并同类项求解;
(2)先去括号,然后合并同类项求解;
(3)先去括号,然后合并同类项求解;
(4)先去括号,然后合并同类项求解.
(2)先去括号,然后合并同类项求解;
(3)先去括号,然后合并同类项求解;
(4)先去括号,然后合并同类项求解.
解答:解:(1)原式=(8-12)a+(7-5)b
=-4a+2b;
(2)原式=5mn-2m+3n-7m-7mn
=-9m+3n-2mn;
(3)原式=3x2y-12xy2-5x2y+xy2
=-2x2y-11xy2;
(4)原式=5a2b-2ab2+3ab2-3a2b
=2a2b+ab2.
=-4a+2b;
(2)原式=5mn-2m+3n-7m-7mn
=-9m+3n-2mn;
(3)原式=3x2y-12xy2-5x2y+xy2
=-2x2y-11xy2;
(4)原式=5a2b-2ab2+3ab2-3a2b
=2a2b+ab2.
点评:本题考查了整式的加减,解答本题的关键是掌握去括号法则和合并同类项法则.

练习册系列答案
相关题目
满足下列条件,不能证明两个三角形全等的是( )
| A、AB=A′B′,∠A=∠A′,AC=A′C′ |
| B、∠A=∠A′,∠B=∠B′,AB=A′B′ |
| C、AB=A′B′,BC=B′C′,AC=A′C′ |
| D、AB=A′B′,∠B=∠B′,AC=A′C′ |
一元二次方程x2+3x=0的根是( )
| A、x=0或x=-3 |
| B、x=0或x=3 |
| C、x=0 |
| D、x=-3 |
下列方程是一元一次方程的是( )
A、
| ||
B、
| ||
| C、y2+2y=-3 | ||
| D、3x-8y=13 |
有下面四包小包装火腿,按规定超过标准克数(200g)的记作正数,不足标准克数的记作负数.其中,最接近标准的是( )
| A、+2 | B、-3 | C、+3 | D、-1 |
下列各式:-
a2b2,
x-1,-25,
,
,π,
,a2-2ab+b2,
中单项式的个数有( )
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| x |
| x-y |
| 2 |
| 2a |
| y | ||
|
| A、5个 | B、4个 | C、3个 | D、2个 |
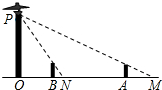 路灯P点距地面9米,身高1.8米的马晓明从距路灯的底部O点20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
路灯P点距地面9米,身高1.8米的马晓明从距路灯的底部O点20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?