题目内容
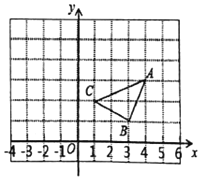
【题目】如图，在平面直角坐标系中，已知
，
，其中
，
满足
，点
为第三象限内一点.
（1）若
到坐标轴的距离相等，
，且
，求
点坐标
（2）若为
，请用含
的式子表示
的面积.
（3）在（2）条件下，当
时，在
轴上有点
，使得
的面积是的面积的2倍，请求出点的坐标.
【答案】（1）
或
；（2）
；（3）
或
.
【解析】
（1）利用M在第三象限且到坐标轴的距离相等，求出M点坐标，同时利用绝对值与算术平方根的非负性求出a、b，得到AB的长度，再利用
，求出N点
（2）利用三角形的面积公式直接写出即可，注意m的取值范围
（3）同（2）利用面积公式写出两个三角形的面积，然后列出方程解方程
（1）由题意可知:
，
求得
，
∵
，
∴
，
，
∴
，
，
∴
，
∵
，，
∴
，
∵
，
∴
或者
，
∴或；
（2）由题意可得：
，
∵
在三象限，
∴
，
∴
；
（3）当
时，
，
由题意可得：
，
，
，
，
∴或.
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
