题目内容
4.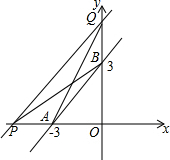 如图所示,在平面直角坐标系中,点A,B的坐标分别为(-3,0),(0,3).一次函数图象与两坐标轴的交点P,Q在直线AB的同侧,且直线PQ与y轴交点在y轴正半轴上,若△QAB和△PAB的面积都等于3,求这个一次函数的解析式.
如图所示,在平面直角坐标系中,点A,B的坐标分别为(-3,0),(0,3).一次函数图象与两坐标轴的交点P,Q在直线AB的同侧,且直线PQ与y轴交点在y轴正半轴上,若△QAB和△PAB的面积都等于3,求这个一次函数的解析式.
分析 根据△PAB与△QAB的面积即可求出PA、QB的长,可得到P、Q的坐标,即可求出直线PQ的解析式.
解答 解:∵点A,B的坐标分别为(-3,0),(0,3).
∴OA=OB=3,
∵S△QAB=3,即$\frac{1}{2}$BQ•AO=3,而AO=3,可求得BQ=2;
∵直线PQ与y轴交点的纵坐标大于3,
∴点Q的坐标为(0,5);
同样可求得PA=2;
由于P、Q两点在直线AB的同侧,
所以点P的坐标为(-5,0);
设直线PQ的解析式为y=kx+b,则$\left\{\begin{array}{l}{-5k+b=0}\\{b=5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=5}\end{array}\right.$,
因此所求一次函数的解析式为y=x+5.
点评 本题考查了待定系数法求一次函数的解析式,根据题意求得P、Q的坐标是解题的关键.

练习册系列答案
相关题目
14.下列条件能说明OC是∠AOB平分线的是( )
| A. | ∠AOC=$\frac{1}{2}$∠AOB | B. | ∠BOC=$\frac{1}{2}$∠AOB | C. | ∠AOC=2∠AOB | D. | ∠AOC=∠AOB |
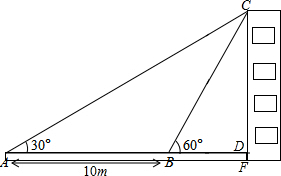 如图,某教学兴趣小组想测量某建筑物的高度,他们在A点测得屋顶C的仰角为30°,然后沿AD方向前进10米,到达B点,在B点测得屋顶C的仰角为60°,已知测量仪AE的高度为1米,请你根据他们的测量数据计算建筑物CF的高度(结果保留根号).
如图,某教学兴趣小组想测量某建筑物的高度,他们在A点测得屋顶C的仰角为30°,然后沿AD方向前进10米,到达B点,在B点测得屋顶C的仰角为60°,已知测量仪AE的高度为1米,请你根据他们的测量数据计算建筑物CF的高度(结果保留根号).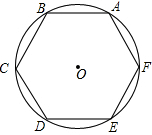 已知正六边形ABCDEF,如图所示,其外接圆的半径是a,求正方形的周长和面积.
已知正六边形ABCDEF,如图所示,其外接圆的半径是a,求正方形的周长和面积. 已知正三角形的边长为a,求它的内切圆与外接圆所围成的圆环的面积.
已知正三角形的边长为a,求它的内切圆与外接圆所围成的圆环的面积.