Question

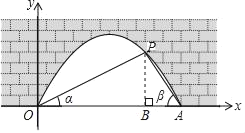
【题目】如图，顶点为的抛物线与轴交于，两点，与轴交于点．

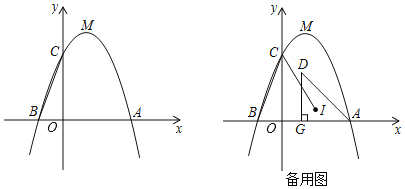
（1）求这条抛物线对应的函数表达式；

（2）问在轴上是否存在一点，使得为直角三角形？若存在，求出点的坐标；若不存在，说明理由．

（3）若在第一象限的抛物线下方有一动点，满足，过作轴于点，设的内心为，试求的最小值．

Answer 1

【答案】（1）；（2）点坐标为或或或时，为直角三角形；（3）最小值为.

【解析】

（1）结合题意，用待定系数法即可求解；

（2）分3种情况讨论，用勾股定理即可求解；

（3）根据正方形的判定和勾股定理，即可得到答案.

（1）∵抛物线过点，，

∴，解得：，

∴这条抛物线对应的函数表达式为.

（2）在轴上存在点，使得为直角三角形．

∵，

∴顶点，

∴，

设点坐标为，

∴，，

①若，则.

∴，

解得：，

∴.

②若，则，

∴，

解得：，，

∴或.

③若，则，

∴，

解得：，

∴.

综上所述，点坐标为或或或时，为直角三角形．

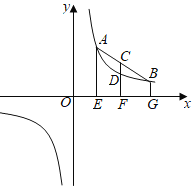
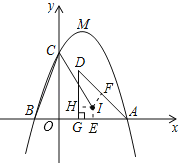
（3）如图，过点作轴于点，于点，于点，

∵轴于点，

∴，

∴四边形是矩形，

∵点为的内心，

∴，，，，

∴矩形是正方形，

设点坐标为，

∴，，

∴，

∵，

∴，

∴，

∵，

∴，

∴化简得：，

配方得：，

∴点与定点的距离为.

∴点在以点为圆心，半径为的圆在第一象限的弧上运动，

∴当点在线段上时，最小，

∵，

∴，

∴最小值为.