题目内容
15. 如图,AC=BC,DC=EC,∠ACB=∠ECD=90°,D为AB边上一点,若AD=1,BD=3.求CD的长.
如图,AC=BC,DC=EC,∠ACB=∠ECD=90°,D为AB边上一点,若AD=1,BD=3.求CD的长.
分析 由于△ACB与△ECD都是等腰直角三角形,于是∠ACE+∠ACD=∠ACD+∠BCD,根据等式性质可得∠ACE=∠BCD,利用SAS可证△ACE≌△BCD,于是∠EAC=∠B=45°,AE=BD=12,易求∠EAD=90°,再利用勾股定理可求DE,进而得到CD的长.
解答 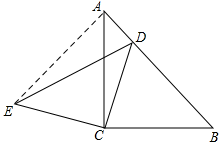 解:连接AE.
解:连接AE.
∵AC=BC,DC=EC,∠ACB=∠ECD=90°,
即∠ACE+∠ACD=∠ACD+∠BCD,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
$\left\{\begin{array}{l}{CD=CE}\\{∠ACE=∠BCD}\\{CB=CA}\end{array}\right.$,
∴△ACE≌△BCD(SAS),
∴∠EAC=∠B=45°,AE=BD=3,
∴∠EAD=∠EAC+∠B=90°,
在Rt△EAD中,DE2=AE2+AD2=32+12=10,
∴DE=$\sqrt{10}$,
∴Rt△DCE中,CD=$\frac{\sqrt{10}}{\sqrt{2}}$=$\sqrt{5}$.
点评 本题考查了全等三角形的判定和性质、勾股定理,解题的关键是先证明△ACE≌△BCD,从而求出AE以及∠EAD=90°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.将抛物线y=-4x2先向左平移2个单位长度,再向下平移5个单位长度,所得到的新的抛物线的解析式为( )
| A. | y=-4(x-2)2-5 | B. | y=-4(x+2)2-5 | C. | y=-4(x-5)2+2 | D. | y=-4(x+5)2-2 |
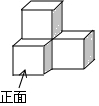 如图是由四个大小相同的正方体组成的几何体,那么它从左面看的形状是( )
如图是由四个大小相同的正方体组成的几何体,那么它从左面看的形状是( )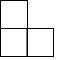
 在△ABC中,AD为角BAC平分线,DE⊥AB于E,DF⊥AC于F,AB=10厘米,AC=8厘米,△ABC的面积为45平分厘米,求DE的长.
在△ABC中,AD为角BAC平分线,DE⊥AB于E,DF⊥AC于F,AB=10厘米,AC=8厘米,△ABC的面积为45平分厘米,求DE的长.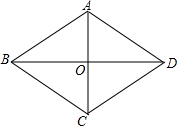 已知:在?ABCD中,对角线AC⊥BD
已知:在?ABCD中,对角线AC⊥BD