题目内容
某园林的门票每张10元,一次使用,考虑到人们的不同需求,也为了吸引更多的游客,该园林除保留原来的售票方法外,还推出了一种“购买个人年票”的售票方法(个人年票从购买日起,可供持票者使用一年),年票分A、B、C三类:A类年票每张120元,持票者进入园林时,无需购买门票;B类年票每张60元,持票者进入该园林时,需再购买门票,每次2元;C类年票每张40元,持票者进入该园林时,需再购买门票,每次3元.
①如果你只选择一种购买门票的方式,并且你计划在一年中用80元花在该园林的门票上,试通过计算,找出可使你进入该园林的次数最多的购票方式.
②求一年中进入该园林至少超过多少次时,购买A类票比较合算.
①如果你只选择一种购买门票的方式,并且你计划在一年中用80元花在该园林的门票上,试通过计算,找出可使你进入该园林的次数最多的购票方式.
②求一年中进入该园林至少超过多少次时,购买A类票比较合算.
考点:一元一次不等式的应用
专题:
分析:①根据题意,需分类讨论.因为80<120,所以不可能选择A类年票;然后计算出若只选择购买B类年票,若只选择购买C类年票,若不购买年票,进入该园林的次数,通过计算发现:可使进入该园林的次数最多的购票方式是选择购买C类年票.
②设一年中进入该园林x次时,购买A类年票比较合算,根据题意,可得不等式组
.求得解集即可得解.
②设一年中进入该园林x次时,购买A类年票比较合算,根据题意,可得不等式组
|
解答:解:①根据题意,需分类讨论.
因为80<120,所以不可能选择A类年票;
若只选择购买B类年票,则能够进入该园林
=10(次);
若只选择购买C类年票,则能够进入该园林
≈13(次);
若不购买年票,则能够进入该园林
=8(次).
所以,计划在一年中用80元花在该园林的门票上,
通过计算发现:可使进入该园林的次数最多的购票方式是选择购买C类年票.
(2)设一年中进入该园林x次时,购买A类年票比较合算,根据题意,
得
.
由①,解得x>30;
由②,解得x>26
;
由③,解得x>12.
解得原不等式组的解集为x>30.
答:一年中进入该园林至少超过30次时,购买A类年票比较合算.
因为80<120,所以不可能选择A类年票;
若只选择购买B类年票,则能够进入该园林
| 80-60 |
| 2 |
若只选择购买C类年票,则能够进入该园林
| 80-40 |
| 3 |
若不购买年票,则能够进入该园林
| 80 |
| 10 |
所以,计划在一年中用80元花在该园林的门票上,
通过计算发现:可使进入该园林的次数最多的购票方式是选择购买C类年票.
(2)设一年中进入该园林x次时,购买A类年票比较合算,根据题意,
得
|
由①,解得x>30;
由②,解得x>26
| 2 |
| 3 |
由③,解得x>12.
解得原不等式组的解集为x>30.
答:一年中进入该园林至少超过30次时,购买A类年票比较合算.
点评:此题主要考查了一元一次不等式组的应用,关键是正确理解题意,找出题目中的不等关系,列出不等式组.

练习册系列答案
相关题目
 如图,直线l1∥l2,若∠1=135°,∠2=65°,则∠3的度数是( )
如图,直线l1∥l2,若∠1=135°,∠2=65°,则∠3的度数是( )| A、70° | B、80° |
| C、65° | D、60° |
 如图,△ABC中AB=2,BC=3,∠B=60°,△ABC的周长是
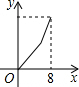
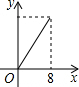
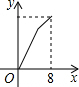
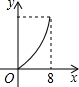
如图,△ABC中AB=2,BC=3,∠B=60°,△ABC的周长是 如图,在长方形ABCD中,CD=5,BC=3,点P从起点D出发沿DC、CB向终点B匀速运动.设点P所走过的路程为x,点P所经过的线段与线段AD、AP所围成图形的面积为y.在下列图象中,能正确反映y与x的函数关系的是( )
如图,在长方形ABCD中,CD=5,BC=3,点P从起点D出发沿DC、CB向终点B匀速运动.设点P所走过的路程为x,点P所经过的线段与线段AD、AP所围成图形的面积为y.在下列图象中,能正确反映y与x的函数关系的是( )