题目内容
13. 如图,△ABC和△DCE都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
如图,△ABC和△DCE都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.(1)找出图中的一对全等三角形,并证明之;
(2)求证:EA⊥AB.
分析 (1)先找出图中的一对全等三角形,然后根据找出的三角形,根据题意可以找出全等的条件,从而可以解答本题;
(2)根据(1)的全等三角形的对应角相等和∠ACB=90°,从而可以证明结论成立.
解答 解:(1)△AEC≌△BDC,
证明:∵△ABC和△DCE都是等腰直角三角形,∠ACB=∠ECD=90°,
∴CE=CD,CA=CB,∠ECA+∠ACD=∠ACD+DCB=90°,
∴∠ECA=∠DCB,
在△AEC和△BDC中,
$\left\{\begin{array}{l}{EC=DC}\\{∠ECA=∠DCB}\\{AC=BC}\end{array}\right.$,
∴△AEC≌△BDC(SAS);
(2)证明:∵△AEC≌△BDC,
∴∠EAC=∠DBC,
又∵∠ACB=90°,
∴∠DBC+∠DAC=90°,
∴∠EAC+∠DAC=90°,
∴∠EAD=90°,
∴EA⊥AB.
点评 本题考查全等三角形的判定与性质、等腰三角形的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.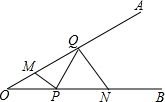 如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )
如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )
 如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )
如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )| A. | β-α=60° | B. | β+α=210° | C. | β-2α=30° | D. | β+2α=240° |
8.等腰△ABC中,若∠A=30°,则其底角等于( )
| A. | 30° | B. | 75° | C. | 30°或75° | D. | 30°或75°或120° |
18.数学兴趣小组的小颖想测量教学楼前的一棵树的高度,下午课外活动时她测得一根长为1米的竹竿的影长是0.8米,测树高时,这棵树在地面上影长为2.6米,请计算树高为( )米.
| A. | 3.25 | B. | 4.25 | C. | 4.45 | D. | 4.75 |
5.下列各组数是勾股数的是( )
| A. | 4,5,6 | B. | 6,8,10 | C. | 5,9,12 | D. | 6,9,13 |
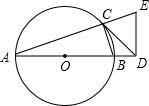 如图,已知点D在⊙O的直径AB延长线上,点C为⊙O上,过D作ED⊥AD,与AC的延长线相交于E,且CD=DE.
如图,已知点D在⊙O的直径AB延长线上,点C为⊙O上,过D作ED⊥AD,与AC的延长线相交于E,且CD=DE.


