Question

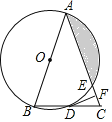
【题目】如图，在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，点E从C点出发向终点B运动，速度为1cm/秒，运动时间为t秒，作EF∥AB，点P是点C关于FE的对称点，连接AP，当△AFP恰好是直角三角形时，t的值为______

Answer 1

【答案】或

【解析】

题中没有已知哪个解是直解，因此分两种情况分别构建方程求解即可．

解：①如图1中，当A、P、E共线时，∠APF=90°，满足条件．

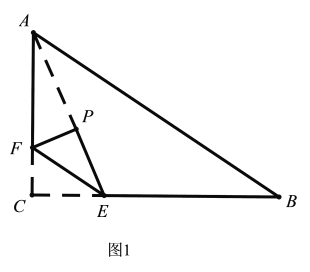
由题意EC=PE=t，CF=PF=t，
由△APF∽△ACE可得==，
∴=，
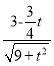解得t=，
②如图2中，当∠PAF=90°时，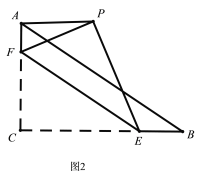

由题意EC=EP=t，CF=PF=t，

易知ED=EB=4-t，PD=PA=2t-4，AF=3-t，
在Rt△PAF中，∵PA2+AF2=PF2，
∴（3-t）2+（2t-4）2=（t）2，
解得t=或2（舍弃），
综上所述，满足条件的t的值为或

故答案为或