题目内容
如图，已知等边△ABC的边长是2cm，将边AC沿射线BC的方向平移2cm，得到线段DE，连接AD、CE
（1）求证：四边形ACED是菱形；
（2）将△ABC绕点C旋转，当CA’与DE交于一点M，CB’与AD交于一点N时，点M、N和点D构成△DMN，试探究△DMN的周长是否存在最小值？如果存在，求出该最小值；如果不存在，请说明理由.
（1）由平移，AD∥CE，AD＝CE，∴四边形ACED是平行四边形…(1分)
又∵AD＝2cm＝AC，∴□ACED是菱形……………………………………………(2分)
（2）连接CD，证得△ACN≌△DCM，…………………………………………………(4分)
证得△CMN是等边三角形，………………………………………………………(5分)
而△DMN的周长即为AD＋CN……………………………………………………(6分)
当CB’⊥AD时，(CN)最小＝
，即△DMN的周长的最小值是2＋…………(8分)
练习册系列答案
相关题目
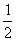∠BOD ，求∠COD的度数．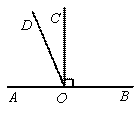
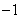，0），B（2，0）两点，与y轴相交于点C．