题目内容
已知抛物线y=ax2+x+c（a≠0）经过A（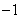
，0），B（2，0）两点，与y轴相交于点C．
（1）求该抛物线的解析式；
（2）点E是该抛物线上一动点，且位于第一象限，当点E到直线BC的距离最大时，求点E的坐标；
（3）在（2）的条件下，在x轴上有一点P，且∠EAO+∠EPO=∠α，当tanα=2时，求点P的坐标．
 |
（1）
（2）设E（
，
），则E到BC距离=
=
E(1,2)
(3)设OP=，若P在正半轴上，则
，
，P(7，0)
若P在负半轴上，则
，
，P(
，0)
练习册系列答案
相关题目
如图是一个三棱柱的图形，它共有五个面，其中三个面是长方形，两个面是三角形，请写出符合下列条件的棱（说明：每个空只需写出一条即可）．
（1）与棱BB1平行的棱： ；
|
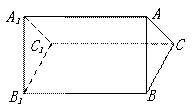（2）与棱BB1相交的棱： ；（3）与棱BB1不在同一平面内的棱： ．
则运算
的最小值为 ．
有一个根为
，且关于x的方程ax 2＋bx＋9＝ 
x
有两个相等的实数根，求
、
的值．
等于 
的解为（ ）
B．
C．
D．
