题目内容
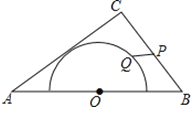
【题目】在![]() 中,
中,![]() ,
,![]() ,以边
,以边![]() 的中点
的中点![]() 为圆心,作半圆与
为圆心,作半圆与![]() 相切,点
相切,点![]() 分别是边
分别是边![]() 和半圆上的动点,连接
和半圆上的动点,连接![]() ,则
,则![]() 长的最大值与最小值的和是__________.
长的最大值与最小值的和是__________.
【答案】9
【解析】
如图,设O与AC相切于点E,连接OE,作OP1⊥BC垂足为P1交O于Q1,此时垂线段OP1最短,P1Q1最小为OP1-OQ1,当Q2在AB边上时,P2与B重合时,P2Q2最大,即可得出答案.
如图所示:

设O与AC相切于点E,连接OE,作OP1⊥BC垂足为P1交 O于Q1,
此时垂线段OP1最短,最小值为OP1-OQ1,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵AO=BO,
∴![]() ,
,
同理可求OE=3,
即![]() ,
,
∴PQ最小值P1Q1=O P1-OQ1=1,
如图,当在AB边上时,与B重合时,P2Q2经过圆心,
∵经过圆心的弦最长,
∴PQ最小值P2Q2=O B-OQ2=3+5=8,
∴PQ长的最大值与最小值的和是1+8=9.
故答案为:9.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目