题目内容
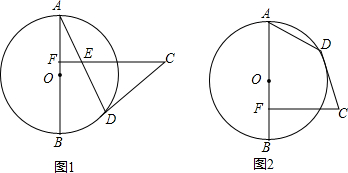
已知AB是⊙O的直径.C是⊙O外的一点,过点C作CD切⊙O于点D.CF⊥AB于F.
(1)如图1,CF交AD于E,求证:CD=CE;
(2)如图2,若tan∠A=2,求sin∠DCF的值.
(1)如图1,CF交AD于E,求证:CD=CE;
(2)如图2,若tan∠A=2,求sin∠DCF的值.

考点:切线的性质
专题:
分析:(1)连接OD,先证出∠ODE+∠CDE=90°,∠A+∠AEF=90°,再证明∠CED=∠CDE,即可得出CD=CE;(2)连接OD,作OE⊥AD,AM⊥OD,由tan∠A=2,设OE=2k,AE=k,得出ED=k,AO=OD=
k,再根据△AOD的面积得出AM、OM,求出∠AOD=∠C,即可得出结论.
| 5 |
解答:解:(1)连接OD;如图1所示:
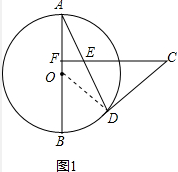 ∵CD是⊙O的切线,
∵CD是⊙O的切线,
∴∠ODC=90°,
∴∠ODE+∠CDE=90°,
∵CF⊥AB,
∴∠A+∠AEF=90°,
∵OA=OD,
∴∠A=∠ODE,
又∵∠AEF=∠CED,
∴∠A+∠CED=∠ODE+∠CDE,
∴∠CED=∠CDE,
∴CD=CE.
(2)连接OD,作OE⊥AD,AM⊥OD,垂足分别为E、M;如图2所示:
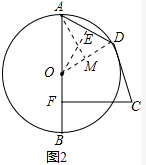 ∵tan∠A=2,设OE=2k,AE=k,
∵tan∠A=2,设OE=2k,AE=k,
则ED=k,AO=OD=
k;
∵
OD•AM=
AD•OE,
∴AM=
k,
∵∠OFC=∠ODC=90°,
∴∠C+∠FOD=180°,
∵∠AOD+∠FOD=180°,
∴∠AOD=∠C,
∴sin∠C=sin∠AOD=
=
=
.
 ∵CD是⊙O的切线,
∵CD是⊙O的切线,∴∠ODC=90°,
∴∠ODE+∠CDE=90°,
∵CF⊥AB,
∴∠A+∠AEF=90°,
∵OA=OD,
∴∠A=∠ODE,
又∵∠AEF=∠CED,
∴∠A+∠CED=∠ODE+∠CDE,
∴∠CED=∠CDE,
∴CD=CE.
(2)连接OD,作OE⊥AD,AM⊥OD,垂足分别为E、M;如图2所示:
 ∵tan∠A=2,设OE=2k,AE=k,
∵tan∠A=2,设OE=2k,AE=k,则ED=k,AO=OD=
| 5 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴AM=
4
| ||
| 5 |
∵∠OFC=∠ODC=90°,
∴∠C+∠FOD=180°,
∵∠AOD+∠FOD=180°,
∴∠AOD=∠C,
∴sin∠C=sin∠AOD=
| AM |
| OA |
| ||||
|
| 4 |
| 5 |
点评:本题考查了切线的性质、等腰三角形的判定与性质以及解直角三角形的知识,运用切线的性质来进行论证或计算,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
|-3|的相反数的倒数是( )
| A、-3 | ||
B、-
| ||
| C、3 | ||
D、
|
 如图,已知线段AB=a(a>1),线段CD=1,线段CD在线段AB上由点A向点B从左向右移动(点C不与点A重合,点D不与点B重合),若设线段AC=x,记图中所有线段的和为S,则S可表示为( )
如图,已知线段AB=a(a>1),线段CD=1,线段CD在线段AB上由点A向点B从左向右移动(点C不与点A重合,点D不与点B重合),若设线段AC=x,记图中所有线段的和为S,则S可表示为( )| A、3a+1 |
| B、2a+1 |
| C、3a+x-1 |
| D、2a+x+1 |
已知点A,B,C在同一直线上,若AB=20cm,AC=30cm,线段BC的长是( )
| A、10cm |
| B、50cm |
| C、25cm |
| D、10cm或50cm |
 如图,已知线段AB=18cm,P在线段AB上,N为PB的中点,且NB=2cm,求PA的长.
如图,已知线段AB=18cm,P在线段AB上,N为PB的中点,且NB=2cm,求PA的长. 点A在DE上,AC=CE,∠1=∠2=∠3,求证:AB=DE.
点A在DE上,AC=CE,∠1=∠2=∠3,求证:AB=DE. 如图,在△ABC中,DE∥BC,S△ADE:S?DBCE=1:2,BC=2
如图,在△ABC中,DE∥BC,S△ADE:S?DBCE=1:2,BC=2