题目内容
18.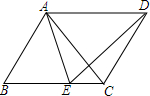 如图,在四边形ABCD中,AD=BC且AD∥BC,E为BC边上一点,且AB=AE.
如图,在四边形ABCD中,AD=BC且AD∥BC,E为BC边上一点,且AB=AE.(1)求证:△ABC≌△EAD;
(2)若AE平分∠DAB,∠EAC=20°,求∠AED的度数.
分析 (1)从题中可知△ABC和△EAD中已经有一条边和一个角分别相等,根据平行的性质和等边对等角得出∠B=∠DAE即可证明.
(2)根据全等三角形的性质,利用平行四边形的性质求解即可.
解答 (1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.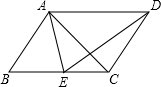
∴∠DAE=∠AEB.
∵AB=AE,
∴∠AEB=∠B.
∴∠B=∠DAE.
∵在△ABC和△AED中,
$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠DAE}\\{AD=BC}\end{array}\right.$,
∴△ABC≌△EAD.
(2)解:∵AE平分∠DAB(已知),
∴∠DAE=∠BAE;
又∵∠DAE=∠AEB,
∴∠BAE=∠AEB=∠B.
∴△ABE为等边三角形.
∴∠BAE=60°.
∵∠EAC=20°,
∴∠BAC=80°.
∵△ABC≌△EAD,
∴∠AED=∠BAC=80°.
点评 本题主要考查了全等三角形的判定及性质.判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL,熟记全等三角形的各种判定方法是解题关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
8.设n为正整数,且n<$\sqrt{11}$<n+1,则n的值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
9.李明同学手中有五张正面分别画有锐角、线段、等腰三角形、圆、四边形的卡片,卡片的形状、大小和背面花色完全相同.李明随机从手中抽取一张,所抽取的图形不是轴对称图形的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
6.下列四个方程中,有一个解为$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$的是( )
| A. | 2x+5y=12 | B. | 3x-y=1 | C. | x+y=1 | D. | 6x+5y=14 |
3.下列事件是确定事件的是( )
| A. | 买彩票中奖 | B. | 走到路口正好是绿灯 | ||
| C. | 掷一枚均匀的骰子,掷出的点数为6 | D. | 早上的太阳从西方升起 |
 关于x的不等式-2x+a≥5的解集如图所示,则a的值是3.
关于x的不等式-2x+a≥5的解集如图所示,则a的值是3.