题目内容
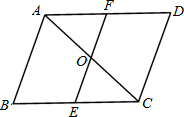已知：平行四边形ABCD中，过对角线AC中点O的直线EF交AD于F，BC于E．求证：BE=DF．
证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴∠FAO=∠ECO，
∵点O是AC的中点，
∴OC=OA，
∴△AOF≌△COE（ASA），
∴AF=CE，
∴BE=FD．
分析：根据平行四边形的性质得出AD∥BC，AD=BC，然后结合点O是AC的中点易证△AOF≌△COE，那么AF=CE，由AD=BC可得BE=DF．
点评：本题考查平行四边形的性质及全等三角形的判定，属于基础题，解答本题要掌握①平行四边形的对边平行且相等，②全等三角形的几个判定定理．
∴AD∥BC，AD=BC，
∴∠FAO=∠ECO，
∵点O是AC的中点，
∴OC=OA，
∴△AOF≌△COE（ASA），
∴AF=CE，
∴BE=FD．
分析：根据平行四边形的性质得出AD∥BC，AD=BC，然后结合点O是AC的中点易证△AOF≌△COE，那么AF=CE，由AD=BC可得BE=DF．
点评：本题考查平行四边形的性质及全等三角形的判定，属于基础题，解答本题要掌握①平行四边形的对边平行且相等，②全等三角形的几个判定定理．
练习册系列答案
相关题目
如图，已知在平行四边形ABCD中，点E在边BC上，射线AE交BD于点G，交DC的延长线于点F，AB=6，BE=3EC，求DF的长．已知在平行四边形ABCD中，向量
=
，
=
，那么向量
等于（ ）
| AB |
| a |
| BC |
| b |
| BD |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
于E，若BP=PD，
如图，已知在平行四边形ABCD中，点E、F分别在边AB、CD上，且AE=2EB，CF=2FD，连接EF．