题目内容
如图，已知在平行四边形ABCD中，点E、F分别在边AB、CD上，且AE=2EB，CF=2FD，连接EF．（1）写出与
| FC |
| AE |
| AE |
（2）填空
| AD |
| EB |
| EF |
| AE |
| FC |
| AE |
| FC |
（3）求作：
| AD |
| FE |
分析：（1）根据平行四边形的对边平行且相等可得AB∥CD，AB=CD，然后求出FC=AE，再根据向量的定义解答；
（2）求出DF=BE，连接AF，根据向量的三角形法则可得
+
=
，再根据-
=
，利用三角形法则求解即可；
（3）过点A作AG∥EF，取AG=EF，根据向量的三角形法则求解即可．
（2）求出DF=BE，连接AF，根据向量的三角形法则可得
| AD |
| EB |
| AF |
| EF |
| FE |
（3）过点A作AG∥EF，取AG=EF，根据向量的三角形法则求解即可．
解答：解：（1）在?ABCD中，AB∥CD，AB=CD，
∵AE=2EB，CF=2FD，
∴AE=
AB=
AB，
CF=
CD=
CD，
∴与
相等的向量是
；
（2）如图，连接AF，
∵DF=CD-FC=
CD，
BE=AB-AE=
AB，
∴
=
，
∴
+
=
，
∵-
=
，
∴
-
=
+
=
，
又∵
=
，
∴
+
-
=
（或
）；
故答案为：（1）
；（2）
或
；
（3）如图，
即为所求作的
-
．
∵AE=2EB，CF=2FD，
∴AE=
| 2 |
| 1+2 |
| 2 |
| 3 |
CF=
| 2 |
| 1+2 |
| 2 |
| 3 |
∴与
| FC |
| AE |
（2）如图，连接AF，
∵DF=CD-FC=
| 1 |
| 3 |
BE=AB-AE=
| 1 |
| 3 |
∴
| EB |
| DF |
∴
| AD |
| EB |
| AF |
∵-
| EF |
| FE |
∴
| AF |
| EF |
| AF |
| FE |
| AE |
又∵
| AE |
| FC |
∴
| AD |
| EB |
| EF |
| AE |
| FC |
故答案为：（1）
| AE |
| AE |
| FC |
（3）如图，
| GD |
| AD |
| FE |
点评：本题考查了平面向量，平行四边形的性质，向量问题熟练掌握平行四边形法则与三角形法则是解题的关键，要注意向量要从方向与大小两个方面考虑求解．
练习册系列答案
阅读快车系列答案
相关题目
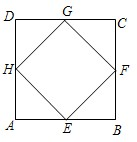四个顶点都在正方形边上的四边形叫做正方形的内接四边形．如图，四边形EFGH是正方形ABCD的内接平行四边形，且已知正方形ABCD的边长为4．
，BO＝AO．又∵AG⊥EB，∠1＋∠3＝
＝∠2＋∠3∴∠1＝∠2，∴Rt△BOE≌Rt△AOF解答此题后某同学产生了如下猜想：对上述命题，若点E在AC的延长线上，AG⊥EB，AG交EB的延长线于G，AG的延长线交DB的延长线于F，其它条件不变，如图，则仍有OE＝OF．问猜想所得的结论是否成立，请说明理由．
