题目内容
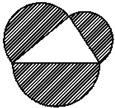
如图，在四边形ABCD中，AB：BC：CD：DA=2：2：3：1，且∠ABC=90°，则∠DAB的度数是______°．
∵AB：BC：CD：DA=2：2：3：1，且∠ABC=90°，
∴AB=BC，
∴∠BAC=∠ACB=45°，
∴AB：BC：AC=2：2：2
=1：1：
，
∴AC：CD：DA=2
：3：1，
∵AC2+AD2=CD2
∴∠DAC=90°，
∴∠DAB=45°+90°=135°．
∴AB=BC，
∴∠BAC=∠ACB=45°，
∴AB：BC：AC=2：2：2
| 2 |
| 2 |
∴AC：CD：DA=2
| 2 |
∵AC2+AD2=CD2
∴∠DAC=90°，
∴∠DAB=45°+90°=135°．
练习册系列答案
阅读快车系列答案
相关题目
