题目内容
12.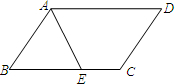 如图所示,在?ABCD中,∠BAD的角平分线AE交BC于点E,AB=4,AD=6,则EC=2.
如图所示,在?ABCD中,∠BAD的角平分线AE交BC于点E,AB=4,AD=6,则EC=2.
分析 根据平行四边形的性质得到AD=BC=6,DC=AB=4,AD∥BC,推出∠DAE=∠BEA,根据AE平分∠BAD,能证出∠BAE=∠BEA,根据等腰三角形的判定得到AB=BE=4,根据EC=BC-BE,代入即可.
解答 解:∵四边形ABCD是平行四边形,
∴AD=BC=6,DC=AB=4,AD∥BC,
∴∠DAE=∠BEA,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BAE=∠BEA,
∴AB=BE=4,
∴EC=BC-BE=6-4=2,
故答案为:2.
点评 本题主要考查了平行四边形的性质,角平分线的定义,平行线的性质,等腰三角形的判定等知识点;熟练掌握平行四边形的性质,证明BE=AB是解决问题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
2.某校有200名学生,要想了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从这2000名学生中抽取了100名学生进行调查,在这次调查中,数据100是( )
| A. | 总体 | B. | 总体的一个样本 | C. | 样本容量 | D. | 全面调查 |
17. 如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )
如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )
 如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )
如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )| A. | 70° | B. | 100° | C. | 140° | D. | 170° |
4.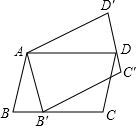 如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C的度数等于( )
如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C的度数等于( )
 如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C的度数等于( )
如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C的度数等于( )| A. | 100° | B. | 105° | C. | 115° | D. | 120° |
2. 如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
 如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )| A. | 逐渐变短 | B. | 先变短后变长 | C. | 先变长后变短 | D. | 逐渐变长 |
 如图是由5个大小相同的小正方体摆成的立体图形,它的左视图是( )
如图是由5个大小相同的小正方体摆成的立体图形,它的左视图是( )


