题目内容
．一张矩形纸片经过折叠得到一个三角形（如图所示），则三角形与矩形周长之比为 ▲ ．
根据折叠的性质得：AC′=DC′=C′F，BC′=BC，
∠1=∠2=∠3，∠4=∠5，∠6=∠7，
∵四边形ABCD是矩形，
∴∠ABC=∠A=90°，
∴∠1=∠2=∠3=
∠ABC=30°，
∴∠4=∠5=180°-∠A-∠1=60°，
∴∠6=∠7=（180°-∠4-∠5）÷2=30°，
设AC′=x，则BC′=2x，C′D=x，
AB=
，C′E=
，BE=
，
∴△BC′E的周长为：C′B+EB+C′E=2x+
，
矩形ABCD的周长为：2（AB+AD）=2×（
）=（
）x，
∴三角形与矩形周长之比为：（
）：（）= ．
∠1=∠2=∠3，∠4=∠5，∠6=∠7，
∵四边形ABCD是矩形，
∴∠ABC=∠A=90°，
∴∠1=∠2=∠3=
∠ABC=30°，∴∠4=∠5=180°-∠A-∠1=60°，
∴∠6=∠7=（180°-∠4-∠5）÷2=30°，
设AC′=x，则BC′=2x，C′D=x，
AB=
，C′E=，BE=，∴△BC′E的周长为：C′B+EB+C′E=2x+
，矩形ABCD的周长为：2（AB+AD）=2×（
）=（）x，∴三角形与矩形周长之比为：（
）：（）= ．
练习册系列答案
相关题目
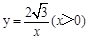图象上一个动点，以P为圆心的圆始终与y轴相切，设切点为A．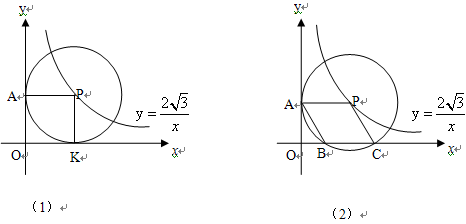
.求腰AB的长.
，求⊙O半径的长度．
是1.7m，看旗杆顶部
的仰角为
；小红的眼睛与地面的距离
是1.5m，看旗杆顶部
．两人相距23m且位于旗杆两侧（点
在同一条直线上）．请求出旗杆
的高度．（参考数据：
，
，结果保留整数）
．