题目内容
有3张扑克牌，分别是红桃3、红桃4和黑桃5．把牌洗匀后甲先抽取一张，记下花色和数字后将牌放回，洗匀后乙再抽取一张．
（1）先后两次抽得的数字分别记为x和y，画出树形图或列表求|x-y|≥1的概率．
（2）甲、乙两人做游戏，现有两种方案．A方案：若两次抽得相同花色则甲胜，否则乙胜．B方案：若两次抽得数字和为奇数则甲胜，否则乙胜．请问甲选择哪种方案胜率更高？
（1）先后两次抽得的数字分别记为x和y，画出树形图或列表求|x-y|≥1的概率．
（2）甲、乙两人做游戏，现有两种方案．A方案：若两次抽得相同花色则甲胜，否则乙胜．B方案：若两次抽得数字和为奇数则甲胜，否则乙胜．请问甲选择哪种方案胜率更高？
考点：列表法与树状图法
专题：计算题
分析：（1）列表得出所有等可能的情况数，找出|x-y|≥1的情况数，即可求出所求的概率；
（2）A方案：找出两次抽得相同花色，以及不同花色的情况，求出甲乙两人获胜的概率；B方案：找出两次抽得数字和为奇数及偶数的情况，求出甲乙两人获胜的概率，比较概率大小即可做出判断．
（2）A方案：找出两次抽得相同花色，以及不同花色的情况，求出甲乙两人获胜的概率；B方案：找出两次抽得数字和为奇数及偶数的情况，求出甲乙两人获胜的概率，比较概率大小即可做出判断．
解答：解：（1）列表如下：
所有等可能的情况有9种，其中|x-y|≥1的情况有6种，
则P=
=
；
（2）A方案：两次抽得相同花色的情况有5种，不同花色的情况有4种，
则P（甲获胜）=
，P（乙获胜）=
；
B方案：两次抽得数字和为奇数的情况有4种，偶数的情况有5种，
则P（甲获胜）=
，P（乙获胜）=
，
则甲选择A方案胜率更高．
| 红桃3 | 红桃4 | 黑桃5 | |
| 红桃3 | （红桃3，红桃3） | （红桃4，红桃3） | （黑桃5，红桃3） |
| 红桃4 | （红桃3，红桃4） | （红桃4，红桃4） | （黑桃5，红桃4） |
| 黑桃5 | （红桃3，黑桃5） | （红桃4，黑桃5） | （黑桃5，黑桃5） |
则P=
| 6 |
| 9 |
| 2 |
| 3 |
（2）A方案：两次抽得相同花色的情况有5种，不同花色的情况有4种，
则P（甲获胜）=
| 5 |
| 9 |
| 4 |
| 9 |
B方案：两次抽得数字和为奇数的情况有4种，偶数的情况有5种，
则P（甲获胜）=
| 4 |
| 9 |
| 5 |
| 9 |
则甲选择A方案胜率更高．
点评：此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
阅读快车系列答案
相关题目
一条排水管的截面如图所示，已知水面宽AB=10cm，截面圆⊙O的半径OC⊥AB于D，且OD：DC=3：2，求⊙O的直径．
如图，点D在AB上，点E在AC上，CD与BE相交于点O，且AD=AE，AB=AC．若∠B=20°，CD=5cm，求∠C的度数和BE的长度．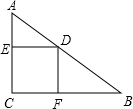
如图，在Rt△ABC中，AC=3cm，BC=4cm，四边形CFDE为矩形，其中CF，CE在两直角边上．设矩形的一边CF=xcm．当x取何值时，矩形ECFD的面积S最大？最大是多少？
如图，一块三角形铁皮，其中∠B=30°，∠C=45°，AC=12