题目内容
如图，在△ABC中，cosB=
| ||
| 2 |
| 3 |
| 5 |
考点：解直角三角形
专题：计算题,数形结合
分析：作AD⊥BC，根据cosB=
，求出∠B=45°，得到BD=AD，根据勾股定理计算出AD、CD的比值，
求出BC的表达式，列出方程解答．
| ||
| 2 |
求出BC的表达式，列出方程解答．
解答：
解：作AD⊥BC，
∵cosB=
，
∴∠B=45°，
∴AD=BD，
∵sinC=
，
设AD=3x，AC=5x，
∴CD=
=4x，
∴BD+CD=7，
∴3x+4x=7，
∴7x=7，
∴x=1，
∴S△ABC=
×7×3=
．
解：作AD⊥BC，∵cosB=
| ||
| 2 |
∴∠B=45°，
∴AD=BD，
∵sinC=
| 3 |
| 5 |
设AD=3x，AC=5x，
∴CD=
| (5x)2-(3x)2 |
∴BD+CD=7，
∴3x+4x=7，
∴7x=7，
∴x=1，
∴S△ABC=
| 1 |
| 2 |
| 21 |
| 2 |
点评：本题考查了解直角三角形，将原三角形化为两个直角三角形是解题的关键．
练习册系列答案
相关题目
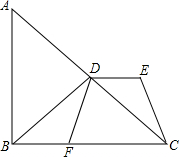在Rt△ABC中，BD是斜边AC的中线，DE∥BF，且DE=BF，试判定四边形DECF的形状．
如图，四边形ABCD是正方形，点G是BC上任意一点，BE⊥AG于点E，点F为AE上一点，且AE-BE=EF，求证：BE∥DF．
如图，一艘货轮由港口A出发向正东方向行驶，在港口A处时，测得灯塔B在港口A的南偏东30°方向，小岛C在港口A的南偏东60°方向，当这艘货轮行驶60海里到点D处时，小岛C恰好在点D处的正南方向，此时测得灯塔B在南偏西60°的方向，求：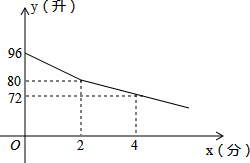
某校部分住校生，放学后到学校锅炉房打水，每人接水2升，他们先同时打开两个放水笼头，后来因故障关闭一个放水笼头．假设前后两人接水间隔时间忽略不计，且不发生泼洒，锅炉内的余水量y（升）与接水时间x（分）的函数图象如图．请结合图象，回答下列问题：
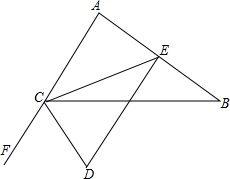如图，已知CE是△ABC的中线，DE⊥AB交外角∠BCF的平分线于D，∠ACB=60°，证明：BC=AC+CD．