题目内容
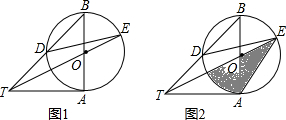
20. 如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.
如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.(1)求证:直线EF是⊙O的切线;
(2)若CF=3,cosA=$\frac{2}{5}$,求出⊙O的半径和BE的长;
(3)连接CG,在(2)的条件下,求$\frac{CG}{EF}$的值.
分析 (1)首先连接OD,由D是BC中点,OC=OA,易得OD是△ABC的中位线,可得OD∥AB,又由DE⊥AB,可得DE⊥OD,即可证得直线EF是⊙O的切线;
(2)由OD∥AB,易得∠COD=∠A,又由CF=3,cosA=$\frac{2}{5}$,设⊙O的半径为R,可得$\frac{R}{R+3}$=$\frac{2}{5}$,则可求得⊙O的半径,则可求得AB的长,继而求得答案;
(3)首先连接CG,易证得CG∥EF,然后由平行线分线段成比例定理,求得答案.
解答 (1)证明:如图,连结OD.
∵CD=DB,CO=OA,
∴OD∥AB,
∵DE⊥AB,
∴DE⊥OD,即OD⊥EF,
∴直线EF是⊙O的切线; (2)解:∵OD∥AB,
(2)解:∵OD∥AB,
∴∠COD=∠A.
在Rt△DOF中,
∵∠ODF=90°,
∴cos∠FOD=$\frac{OD}{OF}$=$\frac{2}{5}$,
设⊙O的半径为R,则$\frac{R}{R+3}$=$\frac{2}{5}$,
解得R=2,
∴AB=2OD=4.
在Rt△AEF中,∵∠AEF=90°,
∴cos∠A=$\frac{AE}{AF}$=$\frac{AE}{4+3}$=$\frac{2}{5}$,
∴AE=$\frac{14}{5}$,
∴BE=AB-AE=4-$\frac{14}{5}$=$\frac{6}{5}$;
(3)解:连接CG,则∠AGC=90°,
∵DE⊥AB,
∴∠AEF=90°,
∴CG∥EF,
∴$\frac{CG}{EF}$=$\frac{AC}{AF}$=$\frac{2R}{2R+CF}$=$\frac{2×2}{2×2+3}$=$\frac{4}{7}$.
点评 此题属于圆的综合题.考查了切线的判定与性质、三角形中位线的性质、平行线分线段成比例定理以及三角函数等知识.注意准确作出辅助线是解此题的关键.

| A. | -7.2×105 | B. | -7.2×104 | C. | 7.2×10-4 | D. | 7.2×10-5 |
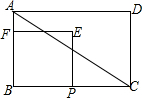 如图,在矩形ABCD中,AB=6,BC=8,点P从点B出发以每秒2个单位长度的速度向终点C运动,点P不与点B重合,以BP为边在BC上方作正方形BPEF,设正方形BPEF与△ABC的重叠部分图形的面积为S(平方单位),点P的运动时间为t(秒).
如图,在矩形ABCD中,AB=6,BC=8,点P从点B出发以每秒2个单位长度的速度向终点C运动,点P不与点B重合,以BP为边在BC上方作正方形BPEF,设正方形BPEF与△ABC的重叠部分图形的面积为S(平方单位),点P的运动时间为t(秒).