题目内容
已知关于 的一元二次方程
的一元二次方程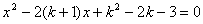 有两个不相等的实数
有两个不相等的实数 根.
根.
(1)求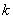 的取值范围;
的取值范围;
(2)当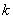 取最小的整数时,求抛物线
取最小的整数时,求抛物线 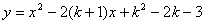 的顶点坐标以及它与
的顶点坐标以及它与 轴的交点坐标;
轴的交点坐标;
(3)将(2)中求得的抛物线在 轴下方的部分沿
轴下方的部分沿 轴翻折到
轴翻折到 轴上方,图象的其余部分不变,得到一个新图象.请你画出这个新图象,并求出新图象与直线
轴上方,图象的其余部分不变,得到一个新图象.请你画出这个新图象,并求出新图象与直线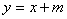 有三个不同公共点时
有三个不同公共点时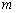 的值.
的值.
解:(1)由题意,得 ,
,
∴ . ∴
. ∴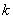 的取值范围为
的取值范围为 . …………2分
. …………2分
(2)∵ ,且
,且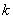 取最小的整数,∴
取最小的整数,∴ .
.
∴ ,
,
则抛物线的顶点坐标为 …………………3分
…………………3分
∵ 的图象与
的图象与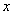 轴相交,
轴相交,
∴ ,∴
,∴ ,
,
∴ 或
或 ,
,
∴抛物线与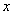 轴相交于
轴相交于
 ,
, . …………4分
. …………4分
(3)翻折后所得新图象如图所示. …………5分
平移直线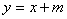 知: 直线位于
知: 直线位于 和
和 时,它与新图象有三
时,它与新图象有三
 个不同的公共点.
个不同的公共点.
①当直线位于 时,此时
时,此时 过点
过点 ,
,
 ∴
∴ ,即
,即 .
.
② 当直线位于 时,此时
时,此时 与函数
与函数
 的图象有一个公共点,
的图象有一个公共点,
∴方程 ,
,
即 有两个相等实根,∴
有两个相等实根,∴ ,
,
即 .
.
当 时,
时, 满足
满足 ,
,
由①②知 或
或 .
.

练习册系列答案
相关题目
 次时,正面向上的概率为______.
次时,正面向上的概率为______.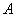 、标杆顶端
、标杆顶端 、树的顶端
、树的顶端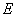 在同一直线上,此同学眼睛距地面1.6
在同一直线上,此同学眼睛距地面1.6 ,标杆长为3.3
,标杆长为3.3 ,
, ,则树高
,则树高

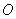 为坐标原点,直线
为坐标原点,直线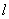 分别交
分别交 轴于
轴于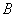 两点,
两点,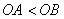 ,且
,且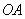 、
、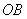 的长分别是一元二次方程
的长分别是一元二次方程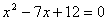 的两根.
的两根.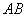 的函数表达式;
的函数表达式;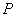 是
是 是第一象限内的点.若以
是第一象限内的点.若以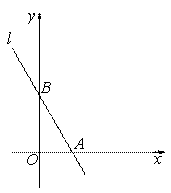





 的分式,满足
的分式,满足 ,所写的分式是: 。
,所写的分式是: 。