题目内容
7. △ABC中,BC=5,AC=12,AB=13,在AB边上有一个动点P,连接PC,作B关于PC的对称点B1,则AB1的最小值是7,当AB1取到最小值时,CP=$\frac{60}{17}$$\sqrt{2}$.
△ABC中,BC=5,AC=12,AB=13,在AB边上有一个动点P,连接PC,作B关于PC的对称点B1,则AB1的最小值是7,当AB1取到最小值时,CP=$\frac{60}{17}$$\sqrt{2}$.
分析 因为B1的变化轨迹是以C为圆心,CB为半径的圆上,所以当B1在AC上时,AB1最小,作PM⊥BC于M,PN⊥AC于N,首先证明四边形MCNP是正方形,设边长为a,再根据$\frac{1}{2}$•BC•AC=$\frac{1}{2}$•AC•PN+$\frac{1}{2}$•BC•PM,列出方程求出a,即可解决问题.
解答 解:因为B1的变化轨迹是以C为圆心,CB为半径的圆上,所以当B1在AC上时,AB1最小,此时AB1=12-5=7,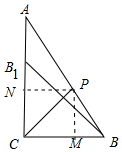
作PM⊥BC于M,PN⊥AC于N,
∵∠PCA=∠PCB,
∴PM=PN,
∵BC=5,AC=12,AB=13,
∴BC2+AC2=AB2,
∴∠ACB=90°,
∵∠MCN=∠PMC=∠PNC=90°,
∴四边形MCNP是矩形,
∵PM=PN,
∴四边形MCNP是正方形,设边长为a,
则有$\frac{1}{2}$•BC•AC=$\frac{1}{2}$•AC•PN+$\frac{1}{2}$•BC•PM,
∴30=$\frac{1}{2}$×12×a+$\frac{1}{2}$×5×a,
∴a=$\frac{60}{17}$,
∴PC=$\sqrt{2}$CM=$\frac{60}{17}$$\sqrt{2}$.
点评 本题考查轨迹,对称变换、勾股定理的逆定理等知识,解题的关键是学会添加常用辅助线,学会利用面积法求有关线段,属于中考常考题型.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
12.下列计算正确的是( )
| A. | (-3)-(-5)=-8 | B. | -5÷$\frac{1}{3}$×$\frac{3}{5}$=-25 | C. | (-3)3=-9 | D. | -22÷(-2)2=-1 |
12.一个整式减去a2-b2等于a2+b2,则这个整式为( )
| A. | 2b2 | B. | 2a2 | C. | -2b2 | D. | -2a2 |
19.某市的出租车的起步价为10元(行驶不超过3千米),以后每增加1千米,加价1.8元,现在某人乘出租车行驶P千米的路程(P>3)所需费用是( )
| A. | 10+1.8P | B. | 1.8P | C. | 10-1.8P | D. | 10+1.8(P-3) |
16.下列说法正确的是( )
| A. | 所有的等腰三角形都是锐角三角形 | |
| B. | 等边三角形属于等腰三角形 | |
| C. | 不存在既是钝角三角形又是等腰三角形的三角形 | |
| D. | 一个三角形里有两个锐角,则一定是锐角三角形 |
17.若等式$\sqrt{2}$□$\sqrt{2}$=2成立,则□内的运算符号是( )
| A. | + | B. | - | C. | × | D. | ÷ |