题目内容
 已知⊙O半径为R
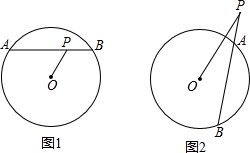
已知⊙O半径为R(1)如图1,过⊙O内一点P作弦AB,连接OP.求证:PA•PB=R2-OP2.
(2)如图2,过⊙O外一点P,作割线PAB,求证:PA•PB=R2-OP2.
考点:切割线定理
专题:证明题
分析:(1)过点P作直径CD,如图1,根据相交弦定理得PA•PB=PC•PD,由于而PC=R-OP,PD=R+OP,则PA•PB=(R-OP)(R+OP),然后利用平方差公式展开即可得到结论;
(2)直线OP交⊙O于C、D,如图2,根据切割线定理得到PA•PB=PC•PD,由于PC=OP-R,PD=OP+R,则PA•PB=(OP-R)(OP+R)=OP2-R2,然后利用平方差公式展开即可得到结论.
(2)直线OP交⊙O于C、D,如图2,根据切割线定理得到PA•PB=PC•PD,由于PC=OP-R,PD=OP+R,则PA•PB=(OP-R)(OP+R)=OP2-R2,然后利用平方差公式展开即可得到结论.
解答:证明:(1)过点P作直径CD,如图1,
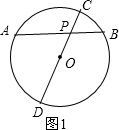 ∵PA•PB=PC•PD,
∵PA•PB=PC•PD,
而PC=OC-OP=R-OP,PD=OD+OP=R+OP,
∴PA•PB=(R-OP)(R+OP)=R2-OP2;
(2)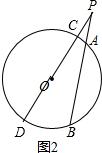 直线OP交⊙O于C、D,如图2,
直线OP交⊙O于C、D,如图2,
∵PCD和PAB都为⊙O的割线,
∴PA•PB=PC•PD,
而PC=OC-OP=OP-R,PD=OD+OP=OP+R,
∴PA•PB=(OP-R)(OP+R)=OP2-R2.
 ∵PA•PB=PC•PD,
∵PA•PB=PC•PD,而PC=OC-OP=R-OP,PD=OD+OP=R+OP,
∴PA•PB=(R-OP)(R+OP)=R2-OP2;
(2)
 直线OP交⊙O于C、D,如图2,
直线OP交⊙O于C、D,如图2,∵PCD和PAB都为⊙O的割线,
∴PA•PB=PC•PD,
而PC=OC-OP=OP-R,PD=OD+OP=OP+R,
∴PA•PB=(OP-R)(OP+R)=OP2-R2.
点评:本题考查了切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等. 也考查了相交弦定理.

练习册系列答案
相关题目
四个角都相等,且邻边相等的四边形是( )
| A、平行四边形 | B、菱形 |
| C、矩形 | D、正方形 |
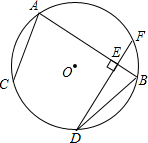 如图,已知AB、AC是⊙O的弦,D为弧BC的中点,弦DF⊥AB于E,AC=2,AB=3,则BE的长为( )
如图,已知AB、AC是⊙O的弦,D为弧BC的中点,弦DF⊥AB于E,AC=2,AB=3,则BE的长为( )| A、1 | ||
B、
| ||
C、
| ||
D、
|
给出下列说法:①0是整数;②-3.2是负分数;③5.6不是正数;④自然数一定是正数;⑤负分数一定是负有理数.其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
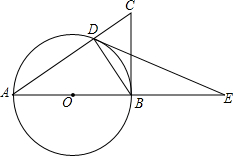 如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,交AC于点D,点E是AB延长线上的一点,且∠BDE=∠A.
如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,交AC于点D,点E是AB延长线上的一点,且∠BDE=∠A.