题目内容
等腰三角形的周长为16,其中一边长为6,则其面积为 .
考点:勾股定理,三角形三边关系,等腰三角形的性质
专题:分类讨论
分析:分①边长6是腰长时,求出底边BC,过点A作AD⊥BC,根据等腰三角形的性质求出BD,再利用勾股定理列式求出AD,然后根据三角形的面积公式列式计算即可得解;②边长6是底边时,求出腰长,再求出BD,然后利用勾股定理列式求出AD,然后利用三角形的面积公式列式计算即可得解.
解答: 解:①边长6是腰长时,如图1,底边BC=16-6×2=4,
解:①边长6是腰长时,如图1,底边BC=16-6×2=4,
过点A作AD⊥BC,则BD=
BC=
×4=2,
由勾股定理得,AD=
=4
,
所以,三角形的面积=
×4×4
=8
;
②边长6是底边时,如图2,腰长AB=
(16-6)=5,
过点A作AD⊥BC,则BD=
BC=
×6=3,
由勾股定理得,AD=
=4,
三角形的面积=
×6×4=12,
综上所述,其面积为8
或12.
故答案为:8
或12.
 解:①边长6是腰长时,如图1,底边BC=16-6×2=4,
解:①边长6是腰长时,如图1,底边BC=16-6×2=4,过点A作AD⊥BC,则BD=
| 1 |
| 2 |
| 1 |
| 2 |
由勾股定理得,AD=
| 62-22 |
| 2 |
所以,三角形的面积=
| 1 |
| 2 |
| 2 |
| 2 |
②边长6是底边时,如图2,腰长AB=
| 1 |
| 2 |
过点A作AD⊥BC,则BD=
| 1 |
| 2 |
| 1 |
| 2 |
由勾股定理得,AD=
| 52-32 |
三角形的面积=
| 1 |
| 2 |
综上所述,其面积为8
| 2 |
故答案为:8
| 2 |
点评:本题考查了勾股定理,等腰三角形的性质,三角形的三边关系,难点在于分情况讨论,作出图形更形象直观.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
不论a为何实数,代数式a2-4a+5的值一定是( )
| A、正数 | B、负数 | C、零 | D、不能确定 |
已知a、b满足(a+2)2+|b-3|=0,则a+b=( )
| A、1 | B、-1 | C、5 | D、-5 |
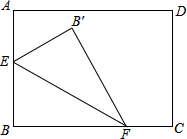 如图,矩形ABCD,AB=3,BC=4,E、F是AB、BC边上的动点,以EF为轴翻折△BEF得△B′EF,连接AB′,求AB′的最小值.
如图,矩形ABCD,AB=3,BC=4,E、F是AB、BC边上的动点,以EF为轴翻折△BEF得△B′EF,连接AB′,求AB′的最小值.