题目内容
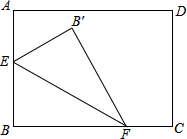 如图,矩形ABCD,AB=3,BC=4,E、F是AB、BC边上的动点,以EF为轴翻折△BEF得△B′EF,连接AB′,求AB′的最小值.
如图,矩形ABCD,AB=3,BC=4,E、F是AB、BC边上的动点,以EF为轴翻折△BEF得△B′EF,连接AB′,求AB′的最小值.考点:翻折变换(折叠问题)
专题:
分析:如图,当点B′在对角线AC上时,线段AB′的值最小,根据勾股定理求出AC的长度,即可解决问题.
解答: 解:如图,当点B′在对角线AC上时,线段AB′的值最小,
解:如图,当点B′在对角线AC上时,线段AB′的值最小,
此时,点F与点C重合;
∵四边形ABCD是矩形,
∴∠B=90°,
由勾股定理得:
AC2=AB2+BC2=9+16=25,
∴AC=5,而B′C=BC=4,
∴AB′=5-4=1.
 解:如图,当点B′在对角线AC上时,线段AB′的值最小,
解:如图,当点B′在对角线AC上时,线段AB′的值最小,此时,点F与点C重合;
∵四边形ABCD是矩形,
∴∠B=90°,
由勾股定理得:
AC2=AB2+BC2=9+16=25,
∴AC=5,而B′C=BC=4,
∴AB′=5-4=1.
点评:该题以矩形为载体,以翻折变换为方法,以考查勾股定理等几何知识点为核心构造而成;解题的关键是借助动态观念,抓住图形在运动过程中暂时静止的某一瞬间,动中求静,以静制动.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,已知△ABC中,AB=AC=12cm,BC=10cm,点D为AB的中点,如果点P在线段AB上以2cm/s的速度由B向C点运动,同时,点Q在先由CA上由C点向A点运动,若运动时间为t秒.
如图,已知△ABC中,AB=AC=12cm,BC=10cm,点D为AB的中点,如果点P在线段AB上以2cm/s的速度由B向C点运动,同时,点Q在先由CA上由C点向A点运动,若运动时间为t秒.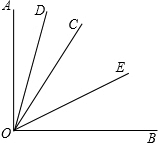 已知:如图,∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.
已知:如图,∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE. 如图所示,线段AB和CD的公共部分为BD,且BD=
如图所示,线段AB和CD的公共部分为BD,且BD=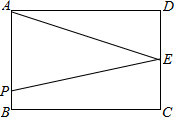 如图,长方形ABCD中,AB=4cm,BC=6cm,点E在边CD上,且DE=2,动点P从A出发,以每秒1cm的速度沿A→B→C→E运动,最终到达点E.若点P的运动时间为x秒,当x为何值时△APE的面积为7?
如图,长方形ABCD中,AB=4cm,BC=6cm,点E在边CD上,且DE=2,动点P从A出发,以每秒1cm的速度沿A→B→C→E运动,最终到达点E.若点P的运动时间为x秒,当x为何值时△APE的面积为7?