题目内容
 从A处观测铁塔顶部的仰角是30°,向前走100米到达B处,观测铁塔的顶部的仰角是45°,求铁塔高.
从A处观测铁塔顶部的仰角是30°,向前走100米到达B处,观测铁塔的顶部的仰角是45°,求铁塔高.考点:解直角三角形的应用-仰角俯角问题
专题:
分析:设铁塔的高度为x米,在Rt△BCD中,根据仰角为45°可得BC=CD=x米,然后在Rt△ACD中用x表示出AC的长度,根据AB=100米,求出x的值即可.
解答:解:设铁塔的高度为x米,
在Rt△BCD中,
∵∠DBC=45°,
∴BC=CD=x,
在Rt△ACD中,
∵∠DAC=30°,
∴
=tan30°=
,
∴AC=
x,
∵AB=100米,
∴
x-x=100,
解得:x=50(
+1)米,
即铁塔的高度为50(
+1)米.
在Rt△BCD中,
∵∠DBC=45°,
∴BC=CD=x,
在Rt△ACD中,
∵∠DAC=30°,
∴
| DC |
| AC |
| ||
| 3 |
∴AC=
| 3 |
∵AB=100米,
∴
| 3 |
解得:x=50(
| 3 |
即铁塔的高度为50(
| 3 |
点评:本题考查了解直角三角形的应用,解答本题的关键是根据仰角构造直角三角形,并解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在如图方格纸中平移四边形ABCD,使点A移到点A′,使点B移到点B′,使点C移到点C′,使点D移到点D′,画出平移后的四边形A′B′C′D′.
在如图方格纸中平移四边形ABCD,使点A移到点A′,使点B移到点B′,使点C移到点C′,使点D移到点D′,画出平移后的四边形A′B′C′D′.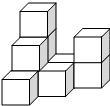 如图,在平整的地面上,有若干个完全相同的棱长为10cm的小正方体堆成一个几何体.
如图,在平整的地面上,有若干个完全相同的棱长为10cm的小正方体堆成一个几何体. 如图,两条直线a,b相交.
如图,两条直线a,b相交.