题目内容
17.①式子4-a2-2ab-b2的最大值是4.②已知a2-5a+1=0,求a2+$\frac{1}{a^2}$=23.
分析 ①逆运用完全平方公式整理,然后即可求解;
②让等式两边同时除以a,得到a+$\frac{1}{a}$=5,两边平方整理即可得到a2+$\frac{1}{{a}^{2}}$的值.
解答 解:①4-a2-2ab-b2=4-(a2+2ab+b2)=4-(a+b)2,
∵(a+b)2≥0,
∴-(a+b)2≤0,
∴当式子(a+b)2=0时,式子4-a2-2ab-b2的最大值是4;
故答案为:4;
②解:∵a2-5a+1=0(a≠0),
∴a+$\frac{1}{a}$=5,
∴(a+$\frac{1}{a}$)2=52,
∴a2+$\frac{1}{{a}^{2}}$=52-2=23,
故答案为:23.
点评 本题考查了完全平方公式,熟记公式是解题的关键.完全平方公式:(a±b)2=a2±2ab+b2.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
9.为了了解某地八年级学生的视力情况,从各类学校中共抽取500名学生的视力进行统计.下列说法正确的是( )
| A. | 这里采用了普查的调查方式 | |
| B. | 调查的总体是某地八年级学生的视力 | |
| C. | 调查的样本是抽取的500名学生 | |
| D. | 调查的总体是500名学生的视力 |
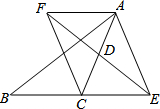 已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE,CF.试猜想线段AF与线段CE有何关系,并说明原因.
已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE,CF.试猜想线段AF与线段CE有何关系,并说明原因.