题目内容
某植物园沿路护栏纹饰部分设计成若干个相同的菱形图案，如图所示，每个菱形的横向对角线长为30cm，每增加一个菱形图案，纹饰长度就增加20cm，当菱形图案的总个数为100时，该纹饰总长度L为__________．
2 010cm．
【考点】菱形的性质．
【分析】根据题意可知，第一个菱形横向对角线长为30cm，以后每增加一个就加20cm，当菱形图案的总个数为100时，总长度L=30+（100﹣1）×20，即可得出结果．
【解答】解：∵以后每增加一个就加dcm，
∴纹饰总长度L=30+（100﹣1）×20=2 010（CM）．
故答案为：2 010cm．
【点评】此题主要考查根据图形找规律，仔细观察图形的变化，找到规律是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
)如图①，小华设计了一个探究杠杆平衡条件的实验:在一根质地均匀的木杆中点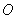
的左侧固定位置
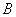处悬挂重物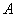
，在中点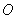的右侧用一个弹簧秤向下拉，改变弹簧秤与点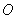的距离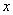
(cm)，观察弹簧秤的示数
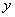（N）的变化情况.实验数据记录如下表:
|
| … | 10 | 15 | 20 | 25 | 30 | … |
|
| … | 30 | 20 | 15 | 12 | 10 | … |
|
第24题
(1)把上表中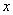、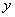的各组对应值作为点的坐标，在平面直角坐标系中(如图②所示)描出相应的点，用平滑的曲线连接这些点并观察所得到的图像，猜测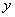（N）与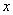 (cm)之间的函数关系，并求出函数表达式.
(2)当弹簧秤的示数为24N时，求弹簧秤与点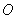的距离.随着弹簧秤与点的距离不断减小，弹簧秤上的示数将发生怎样的变化?
= .
6×103 D．2.96×106
