Question

等腰三角形的腰长为13cm，底边长为10cm，则底边上任意一点到两腰的距离和为________．

Answer 1

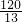cm
分析：先根据三角形的面积公式S_△=×底×高，可求得S_△ABD、S_△ACD、S_△ABC；又由图易知，S_△ABC=S_△ABD+S_△ACD，则DE+DF=CG，然后根据勾股定理得CG²=AC²-AG²=BC²-BG²，设AG=xcm，则列出关于x的方程13²-x²=10²-（13-x）²，解方程求出x的值，进而可求出结果．
解答：如图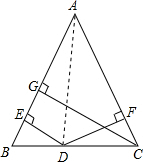，在△ABC中，AB=AC=13cm，BC=10cm，D为BC上任意一点，DE⊥AB，DF⊥AC，垂足为E、F．
连接AD，作CG⊥AB于G．
∵ED⊥AB，∴S_△ABD=AB•ED；
∵DF⊥AC，∴S_△ACD=AC•DF；
∵CG⊥AB，∴S_△ABC=AB•CG；
又∵AB=AC，S_△ABC=S_△ABD+S_△ACD，
∴AB•CG=AB•ED+AC•DF，
∴CG=DE+DF．
设AG=xcm，则BG=（13-x）cm．
由勾股定理，得CG²=AC²-AG²=BC²-BG²，
即13²-x²=10²-（13-x）²，
解得x=9．
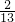则CG²=13²-x²=，
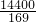CG=．
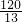所以DE+DF=．
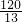故底边上任意一点到两腰的距离和为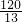cm．
故答案为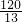cm．
点评：本题主要考查了等腰三角形的性质以及勾股定理的应用．本题考查了等腰三角形的性质、三角形的面积公式等知识点；辅助线的作出是解答本题的关键．