题目内容
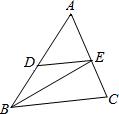 如图,D、E分别是△ABC的边AB、AC的中点,且BE平分∠ABC,DE=2cm,AE=1.5cm,则△ABC的周长是
如图,D、E分别是△ABC的边AB、AC的中点,且BE平分∠ABC,DE=2cm,AE=1.5cm,则△ABC的周长是考点:三角形中位线定理,等腰三角形的判定与性质
专题:
分析:先由三角形中位线定理得出DE∥BC,DE=
BC,再由角平分线定义及平行线的性质得出∠ABE=∠DEB,根据等角对等边得出BD=DE,那么AB=2DE,又AC=2AE,BC=2DE,所以△ABC的周长可求.
| 1 |
| 2 |
解答:解:∵D、E分别是△ABC的边AB、AC的中点,
∴DE∥BC,DE=
BC,AB=2AD,AC=2AE.
∴∠DEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠DEB,
∴BD=DE,
∴AB=2DE=4cm,
又AC=2AE=3cm,BC=2DE=4cm,
∴△ABC的周长=AB+BC+AC=11cm.
故答案为11cm.
∴DE∥BC,DE=
| 1 |
| 2 |
∴∠DEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠DEB,
∴BD=DE,
∴AB=2DE=4cm,
又AC=2AE=3cm,BC=2DE=4cm,
∴△ABC的周长=AB+BC+AC=11cm.
故答案为11cm.
点评:本题考查了三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.同时考查了角平分线定义,平行线的性质,等腰三角形的判定与性质.

练习册系列答案
相关题目
平行四边形是一个不稳定的平面几何图形,现有一个平行四边形的对角线长是8cm和10cm,那么下列数据中符合构成一个平行四边形要求的边长是( )
| A、1cm | B、8cm |
| C、10cm | D、18cm |
下列判断正确的是( )
| A、若ab>0,则a>0,b>0 | ||
| B、若ab<0,则a<0,b>0 | ||
C、若ab>0,则
| ||
| D、若ab<0,则a+b<0 |