题目内容
6.化简:($\frac{{a}^{2}+2a}{a}$-1)÷$\frac{{a}^{2}-1}{2}$.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:原式=$\frac{{a}^{2}+2a-a}{a}$•$\frac{2}{(a+1)(a-1)}$
=$\frac{a(a+1)}{a}$•$\frac{2}{(a+1)(a-1)}$
=$\frac{2}{a-1}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
11.如果关于x的不等式组$\left\{\begin{array}{l}{5x-2a>0}\\{7x-3b≤0}\end{array}\right.$的整数解仅有7,8,9,那么适合这个不等式组的整数a,b的有序数对(a,b)共有( )
| A. | 4对 | B. | 6对 | C. | 8对 | D. | 9对 |
15.4的平方根是( )
| A. | ±4 | B. | ±2 | C. | 2 | D. | -2 |
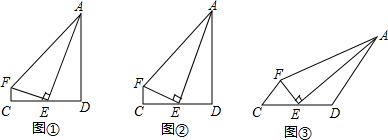
16. 如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(3,4),点C(2,2),点D(3,1),则点D的对应点B的坐标是( )
如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(3,4),点C(2,2),点D(3,1),则点D的对应点B的坐标是( )
 如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(3,4),点C(2,2),点D(3,1),则点D的对应点B的坐标是( )
如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(3,4),点C(2,2),点D(3,1),则点D的对应点B的坐标是( )| A. | (4,2) | B. | (4,1) | C. | (5,2) | D. | (5,1) |
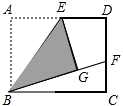 (1)如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为2$\sqrt{6}$.
(1)如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为2$\sqrt{6}$.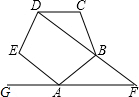 如图,已知正五边形ABCDE,过点A作直线AF∥CD,交DB的延长线于点F
如图,已知正五边形ABCDE,过点A作直线AF∥CD,交DB的延长线于点F