题目内容
14.如图①所示,已知AE⊥FE,垂足为E,且E是DC的中点(1)如图①,如果FC⊥DC,AD⊥DC,垂足分别为C、D,且AD=DC,判断AE是∠FAD的角平分线吗?(不必说明理由)
(2)如图②,如果(1)中的条件去掉“AD=DC”,其余条件不变,(1)中的结论成立吗?请说明理由.
(3)如图③,如果(1)的条件改为,AD∥FC,(1)中的结论仍成立吗?请说明理由.
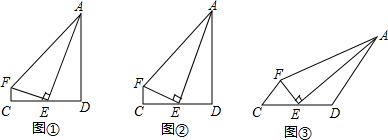
分析 (1)AE是∠FAD的角平分线;延长FE交AD于点B,易证△FCE≌△BDE,则EF=EB,又AE⊥FE,根据线段垂直平分线的性质可得结论;
(2)成立,延长FE交AD于点B,易证△FCE≌△BDE,则EF=EB,又AE⊥FE,根据线段垂直平分线的性质可得结论;
(3)成立,延长FE交AD于点B,证△FCE≌△BDE即可.
解答 解:(1)AE是∠FAD的角平分线;
(2)成立,如图②,延长FE交AD于点B,
∵E是DC的中点,
∴EC=ED,
∵FC⊥DC,AD⊥DC,
∴∠FCE=∠EDB=90°,
在△FCE和△BDE中,
$\left\{\begin{array}{l}{∠FEC=∠DEB}\\{EC=ED}\\{∠FCE=∠EDB}\end{array}\right.$,
∴△FCE≌△BDE,
∴EF=EB,
∵AE⊥FE,
∴AF=AB,
∴AE是∠FAD的角平分线;
(3)成立,如图③,延长FE交AD于点B,
∵AD=DC,
∴∠FCE=∠EDB,
在△FCE和△BDE中,
$\left\{\begin{array}{l}{∠FEC=∠DEB}\\{EC=ED}\\{∠FCE=∠EDB}\end{array}\right.$,
∴△FCE≌△BDE,
∴EF=EB,
∵AE⊥FE,
∴AF=AB,
∴AE是∠FAD的角平分线;
点评 本题主要考查了全等三角形的判定与性质、线段垂直平分线的性质以及等腰三角形三线合一的性质,延长FE交AD于点B,发现△FCE与△BDE一定全等是解决问题的关键.

练习册系列答案
相关题目
2.在一次定点投篮训练中,五位同学投中的个数分别为3,4,4,6,8,则关于这组数据的说法不正确的是( )
| A. | 平均数是5 | B. | 中位数是6 | C. | 众数是4 | D. | 方差是3.2 |
19.若反比例函数y=$\frac{k}{x}$的图象经过点(2,-6),则k的值为( )
| A. | -12 | B. | 12 | C. | -3 | D. | 3 |
3.以下列长度(单位:cm)为边长的三角形是直角三角形的是( )
| A. | 5,6,7 | B. | 7,8,9 | C. | 6,8,10 | D. | 5,7,9 |
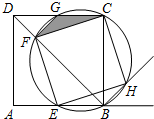 如图,点E是边长为1的正方形ABCD的边AB上任意一点(不含A、B),过B、C、E三点的圆与BD相交于点F,与CD相交于点G,与∠ABC的外角平分线相交于点H.
如图,点E是边长为1的正方形ABCD的边AB上任意一点(不含A、B),过B、C、E三点的圆与BD相交于点F,与CD相交于点G,与∠ABC的外角平分线相交于点H. 如图,在△ABC中,BC=6,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q.当CQ=$\frac{1}{2}$CE时,EP+BP=6;当CQ=$\frac{1}{n}$CE时,EP+BP=6n-6.(用含n的代数式表示)
如图,在△ABC中,BC=6,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q.当CQ=$\frac{1}{2}$CE时,EP+BP=6;当CQ=$\frac{1}{n}$CE时,EP+BP=6n-6.(用含n的代数式表示)