Question

11．如图所示，△ABC中，AB=AC，BD⊥AC于D，BC=6，DC=$\frac{1}{2}$AD，则cosC=$\frac{\sqrt{6}}{6}$．

Answer 1

分析 取AD的中点M，连BM，得到△BCM是等腰三角形，BM=BC，推出△BCM∽△ABC，根据相似三角形的性质得到CM•AC=36，
求得AC=3$\sqrt{6}$，根据三角函数的定义即可得到结论．

解答 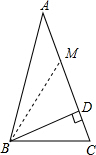解：取AD的中点M，连BM，
∵DC=$\frac{1}{2}$AD=MD，
∴△BCM是等腰三角形，BM=BC，
∴∠ABC=∠C=∠CMB，
∴△BCM∽△ABC，
∴$\frac{CM}{BC}=\frac{BC}{AC}$，
∴CM•AC=36，
∵MC=$\frac{2}{3}$AC，∴AC=3$\sqrt{6}$，
∴cosC=$\frac{CD}{BC}$=$\frac{\frac{1}{3}AC}{BC}$=$\frac{\sqrt{6}}{6}$，
故答案为：$\frac{\sqrt{6}}{6}$．

点评 本题考查了等腰三角形的性质，相似三角形的判定和性质，锐角三角函数的定义，正确的作出辅助线是解题的关键．