题目内容
在△ABC中，tanA=
| ||
| 3 |
| 1 |
| 3 |
| 10 |
考点：解直角三角形
专题：
分析：作CD⊥AB于D，设CD=x，根据勾股定理即可求得CD、BD的长，根据tanA=
，通过解直角三角形即可求得AD的长，进而求得AB．
| ||
| 3 |
解答：解：作CD⊥AB于D，设CD=x，
∵tanB=
，BC=
，
∴BD=3x，
∴x2+（3x）2=BC2，
即10x2=10，解得x=1，
∴CD=1，BD=3，
∵tanA=
，
∴
=
，
∴
=
，解得AD=
，
∴AB=AD+BD=3+
．
故答案为3+
．
∵tanB=
| 1 |
| 3 |
| 10 |
∴BD=3x，
∴x2+（3x）2=BC2，
即10x2=10，解得x=1，
∴CD=1，BD=3，
∵tanA=
| ||
| 3 |
∴
| CD |
| AD |
| ||
| 3 |
∴
| 1 |
| AD |
| ||
| 3 |
| 3 |
∴AB=AD+BD=3+
| 3 |
故答案为3+
| 3 |
点评：本题考查了解直角三角形，勾股定理的应用等，作出辅助线构建直角三角形是本题的关键．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
下列代数式中，单项式共有（ ）
-2ab，
，x+y，x2+y2，-1，
ab2c3．
-2ab，
| 3 |
| x |
| 1 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
如图，数轴上三点A、B、C表示的数分别为a、b、c．且OA=OB，则下列各数：①a+b+c②a+b-c③b+c④b-a-c，其中正数的个数为（ ）
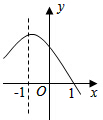抛物线y=ax2+bx+c的对称轴为直线x=-1，与x轴的一个交点为（1，0），部分图象如图所示，若y＞0，则x的取值范围是（ ）| A、-4＜x＜1 |
| B、-3＜x＜1 |
| C、x＜-4或x＞1 |
| D、x＜-3或x＞1 |