题目内容
4.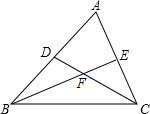 如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,
如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,(1)∠ABC=42°,∠A=60°,求∠BFC的度数;
(2)直接写出∠A与∠BFC的数量关系.
分析 (1)根据角平分线的定义可得∠FBC=$\frac{1}{2}$∠ABC,∠FCB=$\frac{1}{2}$∠ACB,再根据三角形内角和定理求出即可;
(2)根据角平分线的定义可得∠FBC=$\frac{1}{2}$∠ABC,∠FCB=$\frac{1}{2}$∠ACB,然后表示出∠FBC+∠FCB,再根据三角形的内角和等于180°列式整理即可得证.
解答 解:(1)∵∠ABC=42°,∠A=60°,
∴∠ACB=78°,
∵∠ABC、∠ACB的平分线相交于点F,
∴∠FBC=$\frac{1}{2}$∠ABC=21°,∠FCB=$\frac{1}{2}$∠ACB=39°,
∴∠BFC=180°-(∠FBC+∠FCB)=120°;
(2)∠BFC=90°+$\frac{1}{2}$A,
理由是:∵∠ABC与∠ACB的平分线相交于点F,
∴∠FBC=$\frac{1}{2}$∠ABC,∠FCB=$\frac{1}{2}$∠ACB,
∴∠FBC+∠FCB=$\frac{1}{2}$(∠ABC+∠ACB),
在△FBC中,∠BFC=180°-(∠FBC+∠FCB)
=180°-$\frac{1}{2}$(∠ABC+∠ACB)
=180°-$\frac{1}{2}$(180°-∠A)
=90°+$\frac{1}{2}$∠A.
点评 本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.已知△ABC中,AB=4,BC=6,那么边AC的长可能是下列哪个值( )
| A. | 11 | B. | 5 | C. | 2 | D. | 1 |
16. 如图,△ABC≌△DEC,∠A=70°,∠ACB=60°,则∠E的度数为( )
如图,△ABC≌△DEC,∠A=70°,∠ACB=60°,则∠E的度数为( )
 如图,△ABC≌△DEC,∠A=70°,∠ACB=60°,则∠E的度数为( )
如图,△ABC≌△DEC,∠A=70°,∠ACB=60°,则∠E的度数为( )| A. | 70° | B. | 50° | C. | 60° | D. | 30° |
 已知:如图,在等腰△ABC中,AB=AC=20cm,∠C=15°,求腰AC上的高.
已知:如图,在等腰△ABC中,AB=AC=20cm,∠C=15°,求腰AC上的高. 把下列各数分别在数轴上表示出来,并按从大到小的顺序排列,用“>”连接起来.-$\frac{1}{3}$,0,-3,0.2.
把下列各数分别在数轴上表示出来,并按从大到小的顺序排列,用“>”连接起来.-$\frac{1}{3}$,0,-3,0.2.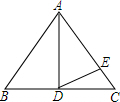 在△ABC中,AB=AC,AD⊥BC,∠BAD=40°,AD=AE.求∠CDE的度数.
在△ABC中,AB=AC,AD⊥BC,∠BAD=40°,AD=AE.求∠CDE的度数.