题目内容
14.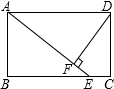 已知:如图,矩形ABCD中,E是BC上一点,DF⊥AE于F,若AE=BC. 求证:BE=AF.
已知:如图,矩形ABCD中,E是BC上一点,DF⊥AE于F,若AE=BC. 求证:BE=AF.
分析 利用矩形的性质对边相等且平行以及每个内角都为90°,进而得出△ABE≌△DFA(AAS),求出即可.
解答 证明:∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BEA,
在△ABE和△DFA中,
$\left\{\begin{array}{l}{∠B=∠DFA}\\{∠BEA=∠FAD}\\{AE=AD}\end{array}\right.$,
∴△ABE≌△DFA(AAS),
∴BE=AF.
点评 此题主要考查了矩形的性质以及全等三角形的判定与性质,得出△ABE≌△DFA是解题关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
8. 如图,将△ABE向右平移2cm得到△DCF.如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
如图,将△ABE向右平移2cm得到△DCF.如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
 如图,将△ABE向右平移2cm得到△DCF.如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
如图,将△ABE向右平移2cm得到△DCF.如果△ABE的周长是16cm,那么四边形ABFD的周长是( )| A. | 16 cm | B. | 18 cm | C. | 20 cm | D. | 21 cm |
9.当b>0时,一次函数y=x+b的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
 直线y=kx+b如图,则关于x的不等式kx+b≤-2的解集是x≥-1.
直线y=kx+b如图,则关于x的不等式kx+b≤-2的解集是x≥-1.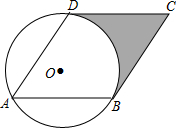 已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.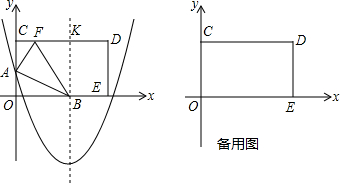
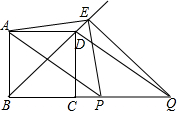 如图,BD是正方形ABCD的对角线,BC=2,动点P从点B出发,以每秒1个单位长度的速度沿射线BC运动,同时动点Q从点C出发,以相同的速度沿射线BC运动,当点P出发后,过点Q作QE⊥BD,交直线BD于点E,连结AP、AE、PE、QE,设运动时间为t(秒).
如图,BD是正方形ABCD的对角线,BC=2,动点P从点B出发,以每秒1个单位长度的速度沿射线BC运动,同时动点Q从点C出发,以相同的速度沿射线BC运动,当点P出发后,过点Q作QE⊥BD,交直线BD于点E,连结AP、AE、PE、QE,设运动时间为t(秒).