题目内容
【题目】如图所示,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与反比例函
,与反比例函![]() 的图象交于点
的图象交于点![]() ,且
,且![]() .
.
(1)求点![]() 的坐标和反比例函数
的坐标和反比例函数![]() 的解析式;
的解析式;
(2)点![]() 在
在![]() 轴上,反比例函数
轴上,反比例函数![]() 图象上存在点
图象上存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形,求点M的坐标.
为平行四边形,求点M的坐标.
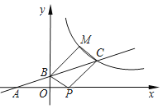
【答案】(1)C(4,2),![]() ;(2)
;(2)![]()
【解析】
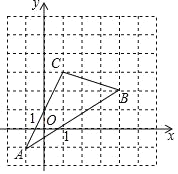
(1)先求A(-4,0), B(0.1),过C作CD⊥x轴于D,得 D(4,0),C(4,2),用待定系数法求解;(2)根据平行四边形性质求G坐标,设M(m,![]() ),P(n.0).则
),P(n.0).则 ,可求交点坐标.
,可求交点坐标.
(1)∵直线![]() 与x轴交于点A,与y轴交于点B.
与x轴交于点A,与y轴交于点B.
∴A(-4,0), B(0.1)
过C作CD⊥x轴于D,
∵AB= BC
∴D(4,0),C(4,2)
∵点C(4.2)反比例函数![]() 的图象上,
的图象上,
∴k=8
∴反比例函数y2的解析式![]()
(2)∵四边形BPCM为平行四边形,
∴G为BC、MP的中点
由BG=CG,则![]()
设M(m,![]() ),P(n.0).
),P(n.0).
又MG=PG
∴
∴![]()


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目