题目内容
12．运动员起跑20m后速度才能达到最大速度10m/s，若运动员的速度是均匀增加的，则他起跑开始到10m处时需要多少s？分析 因为速度是均匀增加，就是匀加速运动，那么它的平均速度=（初始速度+末速度）÷2，初始速度=0m/s，末速度=10m/s，那么平均速度是5m/s，共跑了20÷5=4秒，就是用了4s加速到10m/s，加速度就是10÷4=2.5m/s2（就是每一秒速度快2.5m/s），设10米时速度是x，平均速度就是$\frac{x}{2}$（初始速度为0），共跑了$\frac{20}{x}$秒，已知一秒速度快2.5m/s，$\frac{20}{x}$秒后速度为（即10米处速度为）$\frac{20}{\frac{x}{2.5}}$=$\frac{50}{x}$m/s，由此联立方程求得答案即可．
解答 解：平均速度是（10+0）÷2=5m/s，
共跑了20÷5=4秒，
加速度就是10÷4=2.5m/s2（就是每一秒速度快2.5m/s），
设10米时速度是x m/s，
平均速度就是x=$\frac{x}{2}$（初始速度为0），
共跑了$\frac{10}{\frac{x}{2}}$=$\frac{20}{x}$，
已知一秒速度快2.5m/s，
$\frac{20}{x}$秒后速度为（即10米处速度为）$\frac{20}{\frac{x}{2.5}}$=$\frac{50}{x}$m/s，
则x=$\frac{50}{x}$，
x2=50，
x=5$\sqrt{2}$，
距离是10m，
时间就是$\frac{10}{5\sqrt{2}}$=$\sqrt{2}$s．
答：他起跑开始到10m处时需要$\sqrt{2}$s．
点评 此题考查一元二次方程的实际运用，掌握速度，加速度，时间，路程之间的关系是解决问题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
2．
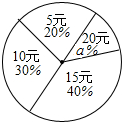尼泊尔地震，波及西藏，人们纷纷献出爱心，某学校学生会向全校1200名学生发起了爱心捐款活动，为了解捐款情况，随机抽查了部分学生的捐款金额，王老师把所得的数据绘制成如图统计图和统计表，请根据相关信息，解答下列问题：
①本次随机抽查的学生人数为50，图中a的值为10；
②求本次调查获取的样本数据的平均捐款为多少？
③根据样本数据，估计该校本次活动捐款为10元的学生人数？
尼泊尔地震，波及西藏，人们纷纷献出爱心，某学校学生会向全校1200名学生发起了爱心捐款活动，为了解捐款情况，随机抽查了部分学生的捐款金额，王老师把所得的数据绘制成如图统计图和统计表，请根据相关信息，解答下列问题：| 金额（元） | 5 | 10 | 15 | 20 |
| 人数 | 10 | 15 | 20 | b |
②求本次调查获取的样本数据的平均捐款为多少？
③根据样本数据，估计该校本次活动捐款为10元的学生人数？
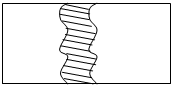如图所示，在一块长为a米，宽为b米的长方形地上，有一条弯曲的柏油马路，马路任何地方的水平宽度都是2米，其他部分都是草地．求草地的面积．
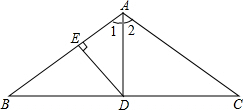如图，在△ABC中，AB=AC，∠C=30°，D是BC边上中点，DE⊥AB于点E，BC=12，求：
