题目内容

16．每个小方格是边长为1个单位长度的小正方形，菱形OABC在平面直角坐标系的位置如图所示．将菱形OABC绕原点O顺时针旋转90°菱形OA1B1C1，请画出菱形OA1B1C1，并求出线段AB旋转到点A1B1所扫过的面积．

分析 根据图形旋转的性质画出图形，再根据勾股定理求出OA及OB的长，根据线段AB旋转到点A1B1所扫过的面积=S扇形BOB1-S扇形OAA1即可得出结论．

解答 解：如图，菱形OA1B1C1即为所求．
∵OA=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$，OB=$\sqrt{{4}^{2}+{4}^{2}}$=$\sqrt{32}$，
∴线段AB旋转到点A1B1所扫过的面积=S扇形BOB1-S扇形OAA1=$\frac{90π×32}{360}$-$\frac{90π×10}{360}$=$\frac{11π}{2}$．

点评 本题考查的是作图-旋转变换，熟知图形旋转不变性的性质是解答此题的关键．

练习册系列答案
相关题目
8．某农户去年承包荒山若干亩，投资7800元改造后，种果树2000棵．今年水果总产量为18000千克，此水果在市场上每千克售a元，在果园每千克售b元（b＜a）．该农户将水果拉到市场出售平均每天出售1000千克，需8人帮忙，每人每天付工资25元，农用车运费及其他各项税费平均每天100元．
（1）分别用a，b表示两种方式出售水果的收入？
（2）若a=1.3元，b=1.1元，且两种出售水果方式都在相同的时间内售完全部水果，请你通过计算说明选择哪种出售方式较好．
（3）该农户加强果园管理，力争到明年纯收入达到15000元，那么纯收入增长率是多少？（纯收入=总收入-总支出，该农户采用了（2）中较好的出售方式出售）
9．计算题
（1）（-7）-（-10）+（-8）-（+2）
（2）-6÷（-$\frac{1}{4}$）×$\frac{11}{24}$
（3）（$\frac{1}{3}$-$\frac{5}{7}$-$\frac{2}{5}$）×105             
（4）-14+[1-（1-0.5×$\frac{1}{3}$）]×[2-（-3）2]．
6．计算
（1）6÷（-2）+|-2|；  
（2）$\root{3}{-8}$+$\sqrt{4}$-14；  
（3）（$\frac{7}{9}$-$\frac{5}{6}$+$\frac{3}{4}$）×（-36）；
（4）（-4）2×$\frac{1}{4}$+23÷（-2）；   
（5）-32×（$\frac{2}{3}$）2+$\frac{4}{9}$÷（-$\frac{2}{3}$）2+$\root{3}{-8}$×（-12014）．

如图，将△ABC沿AB方向向右平移得到△DEF，其中AF=8，DB=2，则平移的距离为（ ）

A. 5 B. 4 C. 3 D. 2
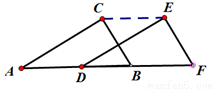
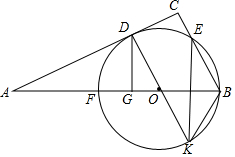20．如图，已知Rt△ABC，∠BCA=90°，以AB边上一点O为圆心，以OB为半径作⊙O交BC于点E；交AB于点F，弧$\widehat{EF}$的中点D在AC上，
（1）证明：AC与⊙O相切；
（2）若CE=1，CD=2，求⊙O的半径；
（3）若$\frac{BE}{BF}$=$\frac{3}{5}$，求$\frac{BC}{DO}$的值．
（4）延长FD交BC的延长线于H点，若DH=6，BF=10，求$\frac{BE}{DE}$的值．
（5）过点D作DG垂直平分OF，G为垂足，作直径DK，连接KE，若EC=2，求△EBK的面积．
7．如图，在平面直角坐标系中，一次函数y=x+1的图象是（　　）
A．B．C．D．
4．如图1，直线y=-3x+3与x，y轴分别交于点A，B．抛物线y=a（x-2）2+n经过点A，B．顶点为P，并与x轴交于另一点C．
（1）求抛物线的表达式：
（2）如图2，点Q在抛物线上，过点Q作QE∥y轴交BC于点E，当QE恰好把△BPC的面积分成1：2的两部分时，求此时点Q的坐标．

规定：M(1)=-2，M(2)=(-2)×(-2)，M(3)=(-2)×(-2)×(-2)，…M(n)=

（1）计算：M(5)+M(6)

（2）求2×M(2015)+M(2016)的值

（3）试说明:2×M(n)与 M(n+1)互为相反数

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网